 Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами
Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами

Геометрическая формулировка:
Изначально теорема была сформулирована следующим образом:
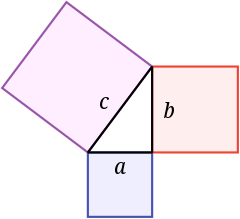
| В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах. |
Алгебраическая формулировка:
| В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. |
То есть, обозначив длину гипотенузы треугольника через  , а длины катетов через
, а длины катетов через  и
и  :
:
Обе формулировки теоремы эквивалентны, но вторая формулировка более элементарна, она не требует понятия площади. То есть второе утверждение можно проверить, ничего не зная о площади и измерив только длины сторон прямоугольного треугольника.
Обратная теорема Пифагора:
Для всякой тройки положительных чисел  ,
,  и
и  , такой, что
, такой, что  , существует прямоугольный треугольник с катетами
, существует прямоугольный треугольник с катетами  и
и  и гипотенузой
и гипотенузой  .
.
Доказательства
На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы[9]. Вероятно, теорема Пифагора является единственной теоремой со столь внушительным числом доказательств. Такое многообразие можно объяснить лишь фундаментальным значением теоремы для геометрии.
Разумеется, концептуально все их можно разбить на малое число классов. Самые известные из них: доказательства методом площадей, аксиоматические и экзотические доказательства (например, с помощью дифференциальных уравнений).
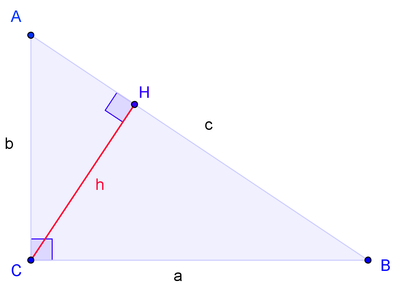
Через подобные треугольники
Следующее доказательство алгебраической формулировки — наиболее простое из доказательств, строящихся напрямую из аксиом. В частности, оно не использует понятие площади фигуры.
Пусть ABC есть прямоугольный треугольник с прямым углом C. Проведём высоту из C и обозначим её основание через H. Треугольник ACH подобен треугольнику ABC по двум углам. Аналогично, треугольник CBH подобен ABC. Введя обозначения
получаем
Что эквивалентно
Сложив, получаем
или
 , что и требовалось доказать
, что и требовалось доказать
Доказательства методом площадей
Ниже приведённые доказательства, несмотря на их кажущуюся простоту, вовсе не такие простые. Все они используют свойства площади, доказательства которых сложнее доказательства самой теоремы Пифагора.
Доказательство через равнодополняемость
- Расположим четыре равных прямоугольных треугольника так, как показано на рисунке 1.
- Четырёхугольник со сторонами c является квадратом, так как сумма двух острых углов 90°, а развёрнутый угол — 180°.
- Площадь всей фигуры равна, с одной стороны, площади квадрата со стороной (a+b), а с другой стороны, сумме площадей четырёх треугольников и площади внутреннего квадрата.
Что и требовалось доказать.
| AB | BC | AC | |
| a) | 9 | 12 | 15 |
| b) | 5 | 11 | 12 |
| c) | 8,8 | 11,7 | 14,8 |
| d) | 5 | 9 | 8 |
| e) | 41 | 9 | 40 |
| f) | 6 | 4,5 | 7,5 |
b) — нет;
c) — да;
d) — нет;
e) — да;
f) — да.
Задача 2 Являются ли треугольники с длиной сторон, указанной ниже, прямоугольными?
b) √3, 3, 2√3;
c) √3, √5, √8.
Ответ: a) — да;
b) — да;
c) — да.
Задача 3 Найдите длину гипотенузы прямоугольного треугольника, если длины двух других сторон равны:
b) √5 и √7;
c) √9 и √11.
Ответ: a) — √5;
b) — √12;
c) — √20.



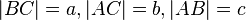


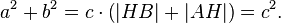

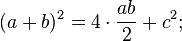
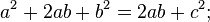










Луценко Александр