Алгебра логики –
это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними.
В данном уроке были использованны материалы с сайта: Фестиваль педагогических идей<
а также картинки были получены мной при помощи запросов на поисковом сервисе, хочешь узнать на каком? перейди по ссылке: «поисковик»<
На страницу урока →
Алгебра логики возникла в середине 19 века в трудах английского математика Джорджа Буля. Ее создание представляло собой попытку решать традиционные логические задачи алгебраическими методами.
Высказывание (суждение)—
это повествовательное предложение, в котором что-либо утверждается или отрицается. По поводу любого высказывания можно сказать истинно оно или ложно.
Определить значения истинности для следующих высказываний.
“Лед — твердое состояние воды”
“Париж-столица Англии”
Истинное высказывание выделить синим маркером,
ложное высказывание красным маркером.
Высказывания бывают общими, частными или единичными. Общее высказывание начинается (или можно начать) со слов: все, всякий, каждый, ни один. Частное высказывание начинается (или можно начать) со слов: некоторые, большинство и т.п. Во всех других случаях высказывание является единичным.
Определить тип высказывания.
“Все рыбы умеют плавать”
“Некоторые медведи — бурые”
“Буква А-гласная”
Общее
Единичное
Частное
В алгебре логики высказывания обозначаются именами логических переменных (А, В, С), которые могут принимать значения истина (1) или ложь (0).
Истина, ложь – логические константы.
Логическое выражение – простое или сложное высказывание. Сложное высказывание строится из простых с помощью логических операции.
Логические операции
Решение задач
Пример 1. Вычислить значение логической формулы: не Х и У или Х и Z, если логические переменные имеют следующие значения: Х=0, У=1, Z=1
Решение. Отметим цифрами сверху порядок выполнения операций в выражении:
1. не 0=1
2. 1 и 1= 1
3. 0 и 1 =0
4. 1 или 0 =1
ответ: 1
Пример 2. Определите истинность формулы не Р или Q и не Р
Построим таблицу истинности
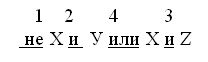
Алексей Петров