Идея доказательства Евклида состоит в следующем: попробуем доказать, что половина площади квадрата, построенного на гипотенузе, равна сумме половин площадей квадратов, построенных на катетах, а тогда и площади большого и двух малых квадратов равны.
Рассмотрим чертеж слева. На нём мы построили квадраты на сторонах прямоугольного треугольника и провели из вершины прямого угла С луч s перпендикулярно гипотенузе AB, он рассекает квадрат ABIK, построенный на гипотенузе, на два прямоугольника — BHJI и HAKJ соответственно. Оказывается, что площади данных прямоугольников в точности равны площадям квадратов, построенных на соответствующих катетах.
Попытаемся доказать, что площадь квадрата DECA равна площади прямоугольника AHJK. Для этого воспользуемся вспомогательным наблюдением: Площадь треугольника с той же высотой и основанием, что и данный прямоугольник, равна половине площади заданного прямоугольника. Это следствие определения площади треугольника как половины произведения основания на высоту. Из этого наблюдения вытекает, что площадь треугольника ACK равна площади треугольника AHK (не изображённого на рисунке), которая, в свою очередь, равна половине площади прямоугольника AHJK.
Докажем теперь, что площадь треугольника ACK также равна половине площади квадрата DECA. Единственное, что необходимо для этого сделать, — это доказать равенство треугольников ACK и BDA (так как площадь треугольника BDA равна половине площади квадрата по указанному выше свойству). Равенство это очевидно: треугольники равны по двум сторонам и углу между ними. Именно — AB=AK, AD=AC — равенство углов CAK и BAD легко доказать методом движения: повернём треугольник CAK на 90° против часовой стрелки, тогда очевидно, что соответствующие стороны двух рассматриваемых треугольников совпадут (ввиду того, что угол при вершине квадрата — 90°).
Рассуждение о равенстве площадей квадрата BCFG и прямоугольника BHJI совершенно аналогично.
Тем самым мы доказали, что площадь квадрата, построенного на гипотенузе, слагается из площадей квадратов, построенных на катетах. Идея данного доказательства дополнительно проиллюстрирована с помощью анимации, расположенной выше.
Данное доказательство также получило название «Пифагоровы штаны».
Доказательство Леонардо да Винчи
Главные элементы доказательства — симметрия и движение.
Рассмотрим чертёж, как видно из симметрии, отрезок  рассекает квадрат
рассекает квадрат  на две одинаковые части (так как треугольники
на две одинаковые части (так как треугольники 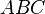 и
и  равны по построению).
равны по построению).
Пользуясь поворотом на 90 градусов против часовой стрелки вокруг точки  , мы усматриваем равенство заштрихованных фигур
, мы усматриваем равенство заштрихованных фигур  и
и  .
.
Теперь ясно, что площадь заштрихованной нами фигуры равна сумме половин площадей маленьких квадратов (построенных на катетах) и площади исходного треугольника. С другой стороны, она равна половине площади большого квадрата (построенного на гипотенузе) плюс площадь исходного треугольника. Таким образом, половина суммы площадей маленьких квадратов равна половине площади большого квадрата, а следовательно сумма площадей квадратов, построенных на катетах равна площади квадрата, построенного на гипотенузе.
Доказательство методом бесконечно малых
Следующее доказательство при помощи дифференциальных уравнений часто приписывают известному английскому математику Харди, жившему в первой половине XX века.
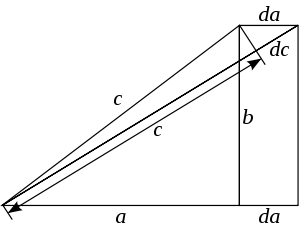
Рассматривая чертёж, показанный на рисунке, и наблюдая изменение стороны a, мы можем записать следующее соотношение для бесконечно малых приращений сторон с и a (используя подобие треугольников):
Пользуясь методом разделения переменных, находим
Более общее выражение для изменения гипотенузы в случае приращений обоих катетов
Интегрируя данное уравнение и используя начальные условия, получаем
Таким образом, мы приходим к желаемому ответу
Как нетрудно видеть, квадратичная зависимость в окончательной формуле появляется благодаря линейной пропорциональности между сторонами треугольника и приращениями, тогда как сумма связана с независимыми вкладами от приращения разных катетов.
Более простое доказательство можно получить, если считать, что один из катетов не испытывает приращения (в данном случае катет  ). Тогда для константы интегрирования получим
). Тогда для константы интегрирования получим
Вариации и обобщения
Подобные геометрические фигуры на трех сторонах
Обобщение теоремы Пифагора сделал Евклид в своей работе Начала, расширив площади квадратов на сторонах до площадей подобных геометрических фигур[10]:
Если построить подобные геометрические фигуры (см. Евклидова геометрия) на сторонах прямоугольного треугольника, тогда сумма двух меньших фигур будет равняться площади большей фигуры.
Главная идея этого обобщения заключается в том, что площадь подобной геометрической фигуры пропорциональна квадрату любого своего линейного размера и в частности квадрату длины любой стороны. Следовательно, для подобных фигур с площадями A, B и C построенных на сторонах с длиной a, b и c, имеем:
Но, по теореме Пифагора, a2 + b2 = c2, тогда A + B = C.
И наоборот, если мы сможем доказать, что A + B = C для трех подобных геометрических фигур без использования теоремы Пифагора, тогда мы сможем доказать саму теорему, двигаясь в обратном направлении. Например, стартовый центральный треугольник может быть повторно использован как треугольник C на гипотенузе, и два подобных прямоугольных треугольника (A и B), построенные на двух других сторонах, которые образуются в результате деления центрального треугольника его высотой. Сумма двух меньших площадей треугольников тогда, очевидно, равна площади третьего, таким образом A + B = C и, выполняя предыдущее доказывания в обратном порядке, получим теорему Пифагора a2 + b2 = c2.
Теорема косинусов
Теорема Пифагора — это частный случай более общей теоремы косинусов, которая связывает длины сторон в произвольном треугольнике:[11]
где θ — угол между сторонами a и b.
Если θ равен 90 градусов, тогда cosθ = 0 и формула упрощается до обычной теоремы Пифагора.
Произвольный треугольник

Обобщение теоремы Пифагора от Сабита ибн Курра.[12] Нижний рисунок: отражение треугольника ABD (сверху), чтобы образовать треугольник DBA, подобный трейгольнику треугольника ABC (верхний).
В любой выбранный угол произвольного треугольника со сторонами a, b, c впишем равнобедренный треугольник таким образом, чтобы равные углы при его основании θ равнялись выбранному углу. Предположим, что выбранный угол θ расположен напротив стороны, обозначенной c. В результате мы получили треугольник ABD с углом θ, что расположен напротив стороны a и стороны r. Второй треугольник образуется углом θ, что расположен напротив стороны b и стороны с длиной s, как показано на рисунке. Сабит Ибн Курра[13] утверждал, что стороны в этих трех треугольниках связаны следующим образом:[14][15]
Когда угол θ приближается к π/2, основание равнобедренного треугольника уменьшается, и две стороны r и s перекрывают друг друга все меньше и меньше. Когда θ = π/2, ADB превращается в прямоугольный треугольник, r + s = c и получаем начальную теорему Пифагора.
Рассмотрим один из доводов. Треугольник ABC имеет такие же углы, как и треугольник ABD, но в обратном порядке. (Два треугольника имеют общий угол при вершине B, оба имеют угол θ и также имеют одинаковый третий угол, по сумме углов треугольника) Соответственно, ABC — подобен отражению ABD треугольника DBA, как показано на нижнем рисунке. Запишем соотношение между противоположными сторонами и прилегающими к углу θ,
Так же отражение другого треугольника,
Перемножим дроби и добавим эти два соотношения:
что и требовалось доказать.
Обобщение для произвольных треугольников через параллелограммы
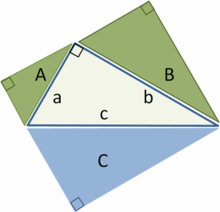
Сделаем дальнейшее обобщение для непрямоугольных треугольников, используя параллелограммы на трех сторонах вместо квадратов.[16] (квадраты — частный случай.) Верхний рисунок демонстрирует, что для остроугольного треугольника площадь параллелограмма на длинной стороне равна сумме параллелограммов на двух других сторонах, при условии что параллелограмм на длинной стороне построен, как изображено на рисунке (размеры, отмеченные стрелками, одинаковые и определяют стороны нижнего параллелограмма). Эта замена квадратов параллелограммами имеет четкое сходство с начальной теоремой Пифагора, считается, что её сформулировал Папп Александрийский в 4 г. н. э.[16]
Нижний рисунок показывает ход доказательства. Посмотрим на левую сторону треугольника. Левый зеленый параллелограмм имеет такую же площадь, как левая часть синего параллелограмма, потому что они имеют такое же основание b и высоту h. Кроме того, левый зеленый параллелограмм имеет такую же площадь, как левый зеленый параллелограмм на верхнем рисунке, потому что они имеют общее основание (верхняя левая сторона треугольника) и общую высоту, перпендикулярную к этой стороне треугольника. Аналогично рассуждая для правой стороны треугольника докажем, что нижний параллелограмм имеет такую же площадь, как у двух зеленых параллелограммов.
Комплексные числа
Теорему Пифагора используют, чтобы найти расстояние между двумя точками в декартовой координатной системе, и эта теорема справедлива для всех истинных координат: расстояние s между двумя точками (a, b) и (c, d) равно
Не возникает проблем с формулой, если к комплексным числам относиться как к векторам с действительными компонентами x + i y = (x, y).. Например, расстояние s между 0 + 1i и 1 + 0i рассчитываем как модуль вектора (0, 1) − (1, 0) = (−1, 1), или
Тем не менее, для операций с векторами с комплексными координатами необходимо провести определенное усовершенствование формулы Пифагора. Расстояние между точками с комплексными числами (a, b) и (c, d); a, b, c, и d все комплексные, сформулируем используя абсолютные величины. Расстояние s основано на векторной разнице (a − c, b − d) в следующем виде:[17] пусть разница a − c = p + i q, где p — действительная часть разницы, q — мнимая часть, и i = √(−1). Аналогично, пусть b − d = r + is. Тогда:
где  — это комплексное сопряженное число для
— это комплексное сопряженное число для  . Например, расстояние между точками (a, b) = (0, 1) и (c, d) = (i, 0), рассчитаем разницей (a − c, b − d) = (−i, 1) и в результате мы бы получили 0, если бы не были использованы комплексные сопряженные. Следовательно, используя усовершенствованную формулу, получим
. Например, расстояние между точками (a, b) = (0, 1) и (c, d) = (i, 0), рассчитаем разницей (a − c, b − d) = (−i, 1) и в результате мы бы получили 0, если бы не были использованы комплексные сопряженные. Следовательно, используя усовершенствованную формулу, получим
Модуль определен следующим образом:
что представляет собой Эрмитово скалярное произведение[18]
Задача 1 В параллелограмме ABCD АВ = 33см, BC = 56 см и АС = 65 см. Проверьте, является ли этот параллелограмм прямоугольником.
Задача 2 Медианы сторон ромба являются вершинами прямоугольника. Если длины сторон прямоугольника есть a и b, какая длина стороны ромба?
Задача 3 Стороны прямоугольника равны 10 см и 24 см. Найти радиус окружности, описанной вокруг прямоугольника.
Задача 4 Гипотенуза прямоугольного треугольника равна 10 cм, а одна из его сторон — 8 cм. Найдите периметр треугольника.
Задача 5 Одна из сторон прямоугольника равна 12 м, а его диагональ — 13 м. Найдите периметр прямоугольника.
Задача 6 Диагонали ромба 10 см и 4 см. Найдите стороны ромба.






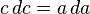







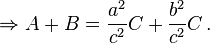

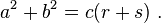

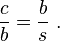




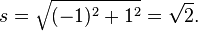
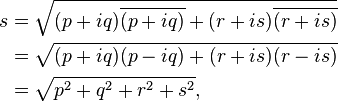











Луценко Александр