Доказательство
Известно, что существует около 350 доказательств теоремы Пифагора. Ниже приведено доказательство, основанное на теореме существования площади фигуры:

- Расположим четыре прямоугольных треугольника так, как показано на рисунке.
- Четырехугольник со сторонами с является квадратом, так как сумма двух острых углов
 , а развернутый угол —
, а развернутый угол —  .
. - Площадь всей фигуры равна, с одной стороны, площади квадрата со стороной (a+b), а с другой стороны — сумме площадей четырех треугольников и внутреннего квадрата.
Что и требовалось доказать.
Задача. Две стороны прямоугольного треугольника равны 6 см и 8 см. Найти третью сторону. (Рассмотреть два случая).
1 случай. Пусть две данные стороны — катеты прямоугольного треугольника.
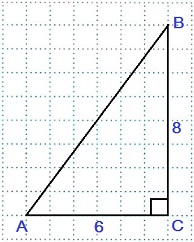 Дано: в Δ АВС / C=90º, АС=6 см, ВС=8 см.
Дано: в Δ АВС / C=90º, АС=6 см, ВС=8 см.
Найти АВ.
Решение. По теореме Пифагора:
АВ²=АС²+ВС²;
АВ²=6²+8²;
АВ²=36+64;
Ответ: АВ=10 см.
Задача. Две стороны прямоугольного треугольника равны 6 см и 8 см. Найти третью сторону. (Рассмотреть два случая).
1 случай. Пусть две данные стороны — катеты прямоугольного треугольника.
 Дано: в Δ АВС / C=90º, АС=6 см, ВС=8 см.
Дано: в Δ АВС / C=90º, АС=6 см, ВС=8 см.
Найти АВ.
Решение. По теореме Пифагора:
АВ²=АС²+ВС²;
АВ²=6²+8²;
АВ²=36+64;
Ответ: АВ=10 см.
решений задач:
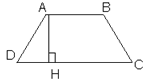
Дано: АВСD – трапеция, АВ и СD – основания. ![]() = 30о, АВ=2 см, СD = 10 см, DA = 8 см.
= 30о, АВ=2 см, СD = 10 см, DA = 8 см.
Найти SАВСD
Решение: так как ![]() = 30о, то АН = 0,5 AD = 4 см.
= 30о, то АН = 0,5 AD = 4 см.
SАВСD = ![]() (2 + 10)×4 = 24 см2.
(2 + 10)×4 = 24 см2.
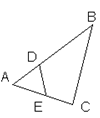
Дано: ![]()
АВ = 8 см, АС = 3 см, АЕ = 2 см. SАВС = 10 см2, SАDE = 2 см2.
Найти AD.
Решение:
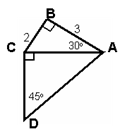
По данным рисунка найдите площадь четырехугольника АВСD.
2. Вычислить:
![]()
3. По данным рисунков найдите угол ![]()
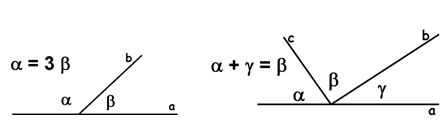
Задача 1 Расстояние по прямой линии от Испериха в Тутракан и Дулово равно 40 км и 28 км соответственно. Соединяя три города, получаем прямой угол в Исперихе. Найдите расстояние от Дулово до Тутракана.
Решение Если искомое расстояние обозначить как x, тогда x2 = 402 + 282 = 1600 + 784 = 2384, x2 = 2384 => x = √2384 ≈ 50 kм.
Задача 2 Докажите, что треугольник со сторонами 3 см, 4 см и 5 см является прямоугольным треугольником.
Решение 32 + 42 = 9 + 16 = 25 = 52. Так как 32 + 42 = 52, то треугольник с такими длинами сторон есть прямоугольным (с гипотенузой 5 cм).


 Теорема
Теорема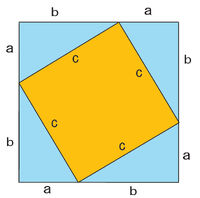











Луценко Александр