Этот урок мы посветим изучению касательной к окружности.
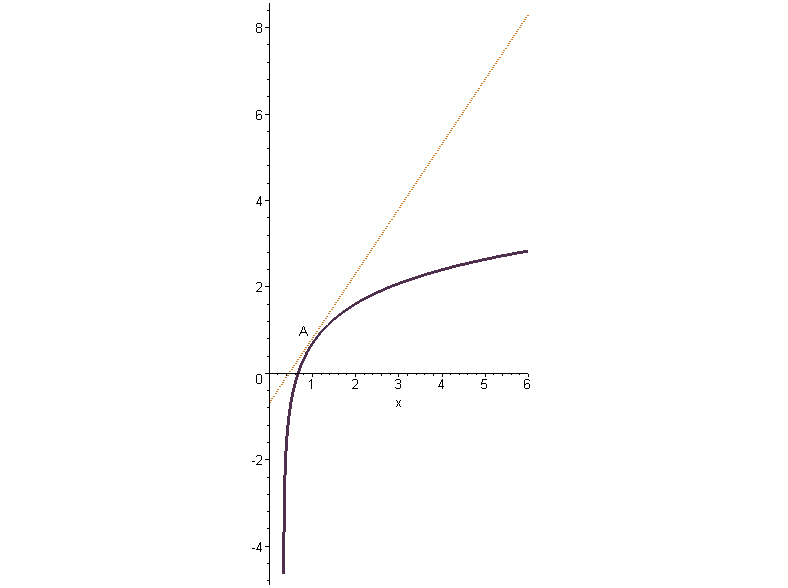
Касательная – это прямая, проходящая через точку кривой, является предельным положением секущей.
Касательная к окружности — это прямая, имеющая с окружностью только одну общую точку, а их общая точка называется точкой касания прямой и окружности.
Какими же свойствами обладает эта прямая?
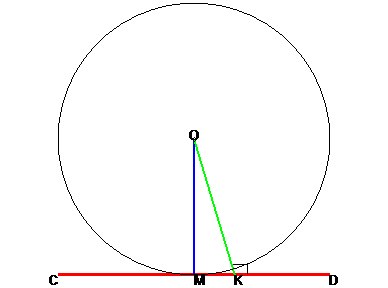
Чтобы ответить на этот вопрос, проведем отрезок соединяющий центр окружности и точку касания, измерим получившийся угол.
Получился угол 90 градусов.
Что можно сказать о касательной и радиусе в точке касания?
Они перпендикулярны.
Теорема 1: Прямая перпендикулярна к радиусу в конечной его точке, лежащей на окружности, является касательной к окружности.
Доказать: CD перпендикулярна касательной к окружности OM.
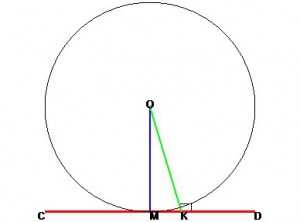
Доказательство: Если OM┴CD, то расстояние от центра О до любой другой точки прямой CD больше радиуса OM. Из этого следует что точка M единственная точка прямой CD и окружности. Поэтому CD касательная к окружности.
Теорема 2: Касательная к окружности перпендикулярна к радиусу этой окружности, проведенная в точке касания.
Наталья Рокотянская