 Многогранники.
Многогранники.
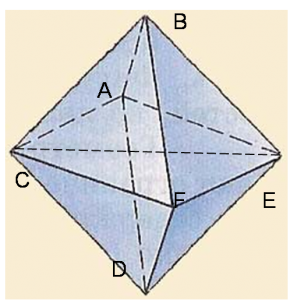
Элементы многогранника
Грани – многоугольники, из которых составлен многогранник (BFE)
Ребра – стороны граней (АВ;CD)
Вершины – концы ребер (А;В;С)
Диагональ – отрезок,
соединяющий две вершины,
одной грани (BD)не принадлежащие
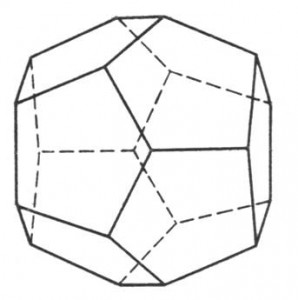
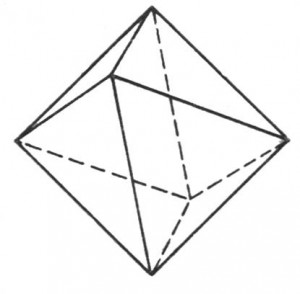
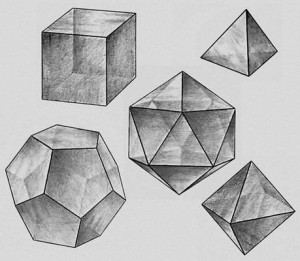
Многогранник называется выпуклым, если он лежит в одной полуплоскости относительно любой грани. Все грани выпуклого многогранника являются выпуклыми многоугольниками. Выпуклый многогранник называется правильным, если его грани являются правильными многоугольниками с одним и тем же числом сторон и в каждой вершине многогранника сходится одно и то же число рёбер. Свойство выпуклого многогранника: Сумма всех плоских углов в его вершине меньше 360 градусов. Теорема Эйлера о числе граней, вершин и ребер выпуклого многогранника: для любого выпуклого многогранника справедливо соотношение Г+В-Р=2, где Г-число граней, В-число вершин, Р-число ребер данного многогранника. Правильные выпуклые многогранники (тела Платона).
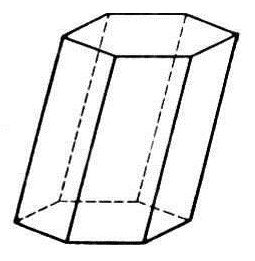
Призма— многогранник, две грани которого являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани -параллелограммами, имеющими общие стороны с этими многоугольниками. Или (равносильно) — это многогранник, в основаниях которого лежат равные многоугольники, а боковые грани —параллелограммы.
Элементы призмы:
| Основания | Боковые ребра | Высота | Диагональ | Боковые грани |
- Основания призмы лежат в параллельных плоскостях.
- Основания призмы равны.
- У призмы боковые ребра параллельны и равны.
- Объём призмы равен произведению её высоты на площадь основания:
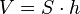
- Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания.
- Площадь боковой поверхности произвольной призмы
 , где
, где  — периметр перпендикулярного сечения,
— периметр перпендикулярного сечения,  — длина бокового ребра.
— длина бокового ребра. - Площадь боковой поверхности прямой призмы
 , где
, где  — периметр основания призмы,
— периметр основания призмы,  — высота призмы.
— высота призмы. - Перпендикулярное сечение перпендикулярно ко всем боковым рёбрам призмы.
- Углы перпендикулярного сечения — это линейные углы двугранных углов при соответствующих боковых рёбрах.
- Перпендикулярное сечение перпендикулярно ко всем боковым граням.
У прямой призмы боковые грани — прямоугольники. Перпендикуляр к плоскостям оснований, концы которого принадлежат этим плоскостям, называют высотой призмы
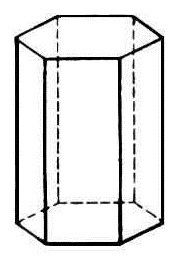
Правильная призма — это призма в основании которой лежит
правильный многоугольник, а боковые ребра перпендикулярны
плоскостям основания.
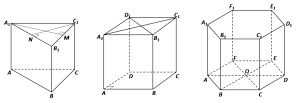
*Боковые грани правильной призмы являются равными прямоугольниками.*Основания правильной призмы являются правильными многоугольниками.
*Правильная призма, боковые грани которой являются квадратами (высота которой равна стороне основания), является полуправильным многогранником
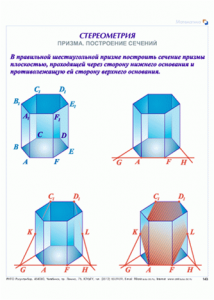
2. Сечение призмы плоскостью, проходящей через два не соседних боковых ребра. В сечении образуется параллелограмм. Такое сечение называется диагональным сечением призмы. В некоторых случаях может получаться ромб, прямоугольник или квадрат.
Сечение правильной призмы.
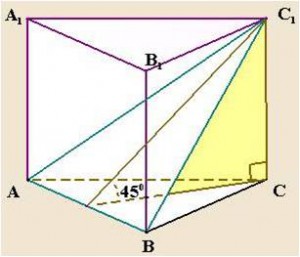
1. Сечение правильной призмы плоскостью, параллельной основанию. В сечении образуется правильный
2. Сечение правильной призмы плоскостью, проходящей через два не соседних боковых ребра. В сечении образуется прямоугольник. В некоторых случаях может образоваться квадрат.многоугольник, равный многоугольнику, лежащему в основании.
Листовка так же привлечёт внимание учеников.
Глоссарий поможет легко ориентироваться ученикам в данной теме. Глоссарий
Презентация. Эта презентация поможет при решение задач по данной теме.Презентация
Можно воспользоваться электронной таблицей .Кроссворд
Для проверки усвоения материала, можно воспользоваться тестом. Тест
ИСТОЧНИКИ:
1.http://geometry.buriks.ru/index.php/Геометрия:Опр.(невыпуклый_многогранник)
2.http://www.mnogograns.narod.ru
3. Л. С. Атанасян и др. Геометрия 10-11 классы: учебник. Изд. “Просвещение”, 2007, 256с.
4.http://dic.academic.ru/dic.nsf/bse/109843/Многогранник
5.http://schools.keldysh.ru/sch1215/data/T_ParalPip.html
















Надира Зизиева