Математическая логика изучает вопросы применения математических методов для решения логических задач и построения логических схем, которые лежат в основе работы любого компьютера.

Суждения в математической логике называют высказываниями или логическими выражениями.
Логическое выражение — это символическая запись, состоящая из логических величин (констант или переменных), объединенных логическими операциями (связками).
В булевой алгебре простым высказываниям ставятся в соответствие логические переменные, значение которых равно 1, если высказывание истинно, и 0, если высказывание ложно.
Обозначаются логические переменные буквами латинского алфавита.
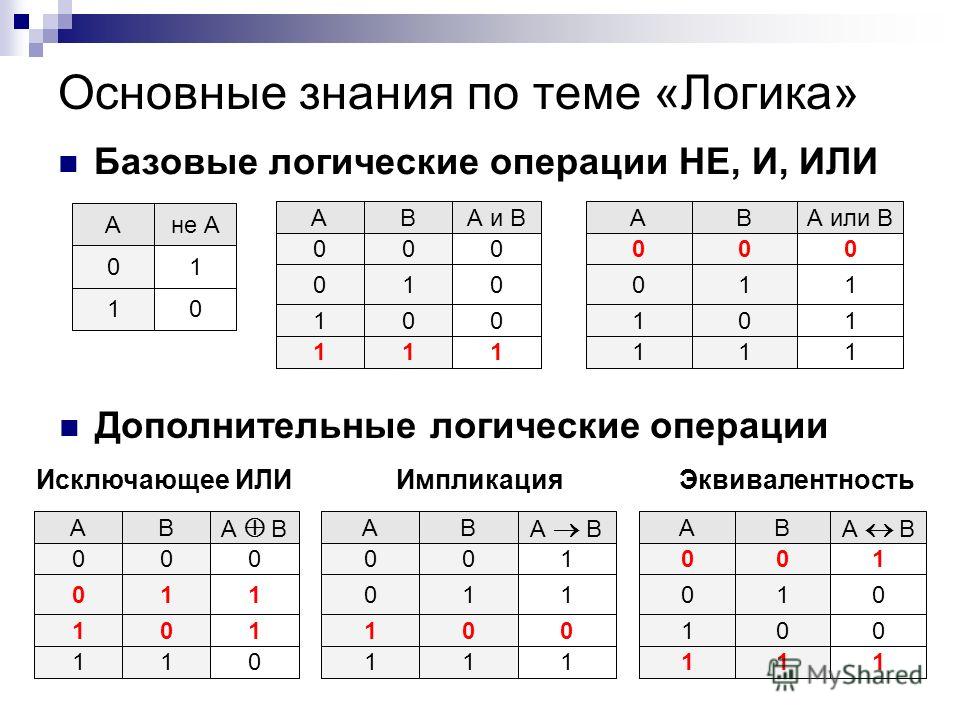
Построение таблиц истинности для логических функций
Логическая функция — это функция, в которой переменные принимают только два значения: логическая единица или логический ноль. Истинность или ложность сложных суждений представляет собой функцию истинности или ложности простых. Эту функцию называют булевой функцией суждений f (a, b).
Любая логическая функция может быть задана с помощью таблицы истинности, в левой части которой записывается набор аргументов, а в правой части — соответствующие значения логической функции.
При построении таблицы истинности необходимо учитывать порядок выполнения логических операций. Операции в логическом выражении выполняются слева направо с учетом скобок в следующем порядке:
1. инверсия;
2. конъюнкция;
3. дизъюнкция;
4. импликация и эквивалентность.
Алгоритм построения таблицы истинности
1. Определить количество наборов входных переменных — всевозможных сочетаний значений переменных, входящих в выражения, по формуле: Q=2n , где n — количество входных переменных. Оно определяет количество строк таблицы.
2. Внести в таблицу все наборы входных переменных.
3. Определить количество логических операций и последовательность их выполнения.
4. Заполнить столбцы результатами выполнения логических операций в обозначенной последовательности.

Чтобы не повторить или не пропустить ни одного возможного сочетания значений входных переменных, следует пользоваться одним способов заполнения таблицы.
Каждый набор значений исходных переменных есть код числа в двоичной системе счисления, причем количество разрядов числа равно количеству входных переменных. Первый набор — число 0. Прибавляя к текущему числу каждый раз по 1, получаем очередной набор. Последний набор — максимальное значение двоичного числа для данной длины кода.
Например, для функции от трех переменных последовательность наборов состоит из чисел:
| 000 |
| 001 |
| 010 |
| 011 |
| 100 |
| 101 |
| 110 |
| 111 |
Логические функции и их преобразования. Законы логики
Для операций конъюнкции, дизъюнкции и инверсии определены законы булевой алгебры, позволяющие производить тождественные (равносильные) преобразования логических выражений.
Законы логики
1. ¬¬ А <=> A закон двойного отрицания;
2. A&B <=> B&A коммутативность конъюнкции;
3. AVB <=> BVA коммутативность дизъюнкции;
4. A&(B&C) <=> (A&B)&C ассоциативность конъюнкции;
5. AV(BVC) <=> (AVB)VC ассоциативность дизъюнкции;
6. A&(BVC) <=> (A&B)V(A&C) дистрибутивность конъюнкции относительно дизъюнкции;
7. AV(B&C) <=> (AVB)&(AVC) дистрибутивность дизъюнкции относительно конъюнкции;
8. A&A <=> A
9. AVA <=> A
10. AV¬A <=> И закон исключенного третьего;
11. A&¬A <=> Л закон непротиворечия;
12. A&И <=> A
13. AVИ <=> И
14. A&Л <=> Л
15. AVЛ <=> A
16. ¬(A&B) <=> ¬ A V ¬ B законы де Моргана;
17. ¬(AVB) <=> ¬ A & ¬ B
18. A => B <=> ¬ A V B замена импликации.
Основываясь на законах, можно выполнять упрощение сложных логических выражений. Такой процесс замены сложной логической функции более простой, но равносильной ей, называется минимизацией функции.
Вопросы для самоконтроля
- Основные логические операции: конъюнкция, дизъюнкия (оба вида), отрицание, импликация, эквивалентность. Примеры логических выражений.
- Таблица истинности. Примеры. A and not A; A or not A.
- Законы логики.












Анна Лукина