Ломаной называется фигура, которая состоит из точек и соединяющих их отрезков.
Точки называются вершинами ломаной, а отрезки — звеньями ломаной.
Виды ломаных
Ломаная называется замкнутой, если у неё концы совпадают.
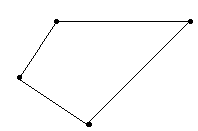
Если концы ломаной не совпадают, то она называется незамкнутой.
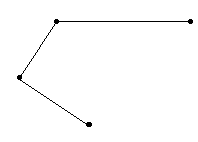
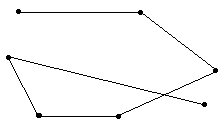
Ломаная называется простой, если она не имеет самопересечений. Обе ломаные выше являются простыми.
На следующем рисунке ломаная с самопересечением.
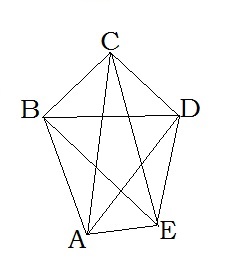
Многоугольник — это простая замкнутая ломаная линия и конечная часть
плоскости, которую она ограничивает.
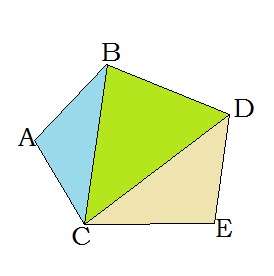
Вершины ломаной линии называются вершинами многоугольника, а её звенья — сторонами многоугольника.
Отрезок, соединяющий две вершины, не лежащие на одной стороне, называется диагональю многоугольника.
A , B, C, D, E — вершины;
AB, BC, CD, DE, AE — стороны;
AC, AD, BE, BD, CE — диагонали.
Многоугольник, у которого все углы меньше 180°, называется выпуклым многоугольником.
Пятиугольник ABCDE является выпуклым многоугольником.
Сумма углов выпуклого n-угольника
В общем случае многоугольник можно назвать n-угольником, это означает, что у данного многоугольника n сторон и n вершин.
Сумма углов выпуклого n-угольника равна 180°⋅(n−2)
Сумма внутренних углов любого треугольника равна 180°.
Поэтому сумма углов выпуклого n-угольника равна 180°⋅(n−2).
Пример:
Вычисли сумму внутренних углов выпуклого одиннадцатиугольника.
Используем формулу:
180°⋅(n−2)=?
Чекина Арина