Отрицательные числа
Дать определение отрицательных чисел нам поможет координатная прямая.
Координатная прямая — это прямая на которой: отмечена точка, принятая за начало отсчета, положительное направление этой прямой и масштаб — единичный отрезок.

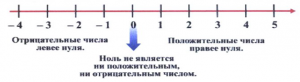
Определение. Числа, которые соответствуют точкам координатной прямой, лежащим правее начала отсчета, называют положительными.
Определение. Числа, которые соответствуют точкам координатной прямой, лежащим левее начала отсчета называю отрицательными.
Число нуль, соответствующее началу отсчета, не является ни положительным, ни отрицательным числом.
Числа 3 и -3; 5 и -5; 11,9 и -11,9; 4/5 и- 4/5 называются противоположными.
Модуль числа

Координата точки М равна – 4. Расстояние от точки М до начала координат О равно четырем единичным отрезкам.
Число 4 называют модулем числа – 4. Пишут: 4 = | – 4 | .
Модуль числа 4 равен 4 , так как точка N удалена от начала отсчета на четыре единичных отрезка. Пишут: | 4 | = 4 .
Модулем числа a называют расстояние (в единичных отрезках) от начала координат до точки a .
Модуль числа 0 равен 0. Модуль числа не может быть отрицательным.
Для положительного числа и нуля он равен самому числу, а для отрицательного — противоположному числу.
Противоположные числа имеют равные модули: | – a | = | a |.

Рассмотрим внимательно примеры:

Сравнение отрицательных чисел
Что больше:-1 или -2? Изобразим на числовой прямой эти координаты:

Итак, если сравнивать числа с помощью горизонтальной координатной прямой, из двух чисел меньшим считается то, изображение которого на координатной прямой расположено левее, а большим то, изображение которого расположено правее.
Число -2 стоит левее числа -1, значит, оно меньше -1>-2
На координатной прямой положительные числа располагаются справа от нуля, а отрицательные – слева от нуля, всякое положительное число больше нуля, а всякое отрицательное меньше нуля, и поэтому всякое отрицательное число меньше всякого положительного числа.
Если же мы сравниваем два отрицательных числа, то нужно сравнить их модули: большим будет то число, модуль которого меньше, а меньшим то число, модуль которого меньше. Например, -7 и -5. Сравниваемые числа – отрицательные. Сравниваем их модули 5 и 7. 7 больше чем 5, значит -7 меньше чем -5. Если отметить на координатной прямой два отрицательных числа, то левее окажется меньшее число, а большее будет расположено правее. -7 расположено левее -5, значит -7 < -5.
Дать определение отрицательных чисел нам поможет координатная прямая.
Координатная прямая — это прямая на которой: отмечена точка, принятая за начало отсчета, положительное направление этой прямой и масштаб — единичный отрезок.

Определение. Числа, которые соответствуют точкам координатной прямой, лежащим правее начала отсчета, называют положительными.
Определение. Числа, которые соответствуют точкам координатной прямой, лежащим левее начала отсчета называю отрицательными.
Число нуль, соответствующее началу отсчета, не является ни положительным, ни отрицательным числом.

Числа 3 и -3; 5 и -5; 11,9 и -11,9; 4/5 и- 4/5 называются противоположными.
Модуль числа
Координата точки М равна – 4. Расстояние от точки М до начала координат О равно четырем единичным отрезкам.
Число 4 называют модулем числа – 4. Пишут: 4 = | – 4 | .
Модуль числа 4 равен 4 , так как точка N удалена от начала отсчета на четыре единичных отрезка. Пишут: | 4 | = 4 .
Модулем числа a называют расстояние (в единичных отрезках) от начала координат до точки a .
Модуль числа 0 равен 0. Модуль числа не может быть отрицательным.
Для положительного числа и нуля он равен самому числу, а для отрицательного — противоположному числу.
Противоположные числа имеют равные модули: | – a | = | a |.

Рассмотрим внимательно примеры:

Сравнение отрицательных чисел
Что больше:-1 или -2? Изобразим на числовой прямой эти координаты:
Итак, если сравнивать числа с помощью горизонтальной координатной прямой, из двух чисел меньшим считается то, изображение которого на координатной прямой расположено левее, а большим то, изображение которого расположено правее.
Число -2 стоит левее числа -1, значит, оно меньше -1>-2
На координатной прямой положительные числа располагаются справа от нуля, а отрицательные – слева от нуля, всякое положительное число больше нуля, а всякое отрицательное меньше нуля, и поэтому всякое отрицательное число меньше всякого положительного числа.
Если же мы сравниваем два отрицательных числа, то нужно сравнить их модули: большим будет то число, модуль которого меньше, а меньшим то число, модуль которого меньше. Например, -7 и -5. Сравниваемые числа – отрицательные. Сравниваем их модули 5 и 7. 7 больше чем 5, значит -7 меньше чем -5. Если отметить на координатной прямой два отрицательных числа, то левее окажется меньшее число, а большее будет расположено правее. -7 расположено левее -5, значит -7 < -5.
Презентация по теме:prez1










Екатерина Чимаева (Матвеенко)