Сегодня нам предстоит повторить все, что изучили о площадях известных фигур (прямоугольник, квадрат, параллелограмм, ромб). Вывести формулу для площади треугольника и научиться решать задачи.
На страницу урока →
ПЛОЩАДЬ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА
Площадь прямоугольного треугольника равна половине произведения катетов.
ПЛОЩАДЬ ЛЮБОГО ТРЕУГОЛЬНИКА
Площадь любого треугольника равна половине произведения основания на высоту.
ТЕОРЕМА ПИФАГОРА
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
1) Катеты прямоугольного треугольника равны 25 и 28. Найти площадь треугольника.
1) 350
2) 35
3) 700
4) 70
2) Катет и гипотенуза прямоугольного треугольника соответственно равны 40 и 41. Найти площадь треугольника.
1)1640
2) 820
3) 180
4) 18
3) Найти площадь треугольника, если высота, проведённая к основанию равна 10 , а основание 18.
1)45
2) 90
3) 180
4) 450
4) Боковая сторона равнобедренного треугольника равна 25, а основание равно 40. Найти площадь треугольника.
1)600
2) 60
3) 30
4) 300
5) Площадь треугольника равна 119, а высота 17. Найти основание.
1)7
2) 14
3) 28
4) 3,5
6) В треугольнике АВС высоты АК и ВН равны 6 и 4, а сторона ВС равна 10. Найти сторону АС треугольника.
1) 7,5
2) 15
3) 2,4
4) 5
7) Средняя линия треугольника равна 22, высота проведенная к стороне параллельной этой средней линии 18. Найти площадь треугольника
1) 396
2) 198
3) 96
4) 792
8) Сторона равностороннего треугольника равна 2
Найти площадь треугольника.
1) 12
2) 12
3) 9
4) 3
9) Угол при основании равнобедренного треугольника равен 
, а боковая сторона 
. Найти площадь треугольника.
1) 1
2)
3) 2
4) 2
10) В тупоугольном треугольнике один угол 
, а стороны, заключающие этот угол равны 18 и 12. Найти площадь треугольника
1)108
2) 54
3) 27
4) 216
ЗАДАЧИ
№ 493
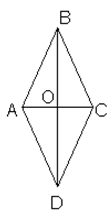
Дано: АВСD-ромб. АС = 10 см, BD = 24 см.
Найти АВ, площадь ромба
№ 494
Дано: АВСD-ромб. АВ = 10 см, АС = 12 см.
Найти BD, Sромба
Решение:
ДОМАШНЕЕ ЗАДАНИЕ
- провести полное доказательство теоремы Пифагора путем достроения треугольника до квадрата со стороной (а + b).
- индивидуальное задание сильным учащимся – найти и подготовить другие доказательства теоремы Пифагора.
- Уметь доказывать теорему одним из способов.
- Решить задачи: № 483 (а; б), № 484 (б, г), № 487.
- дополнительное творческое задание (по желанию): придумайте сами чертеж к задаче, где для решения применялась бы теорема Пифагора (можно использовать комбинации различных фигур – прямоугольника, ромба, трапеции, прямоугольного треугольника). Предложите свою задачу классу.
ИСТОЧНИКИ
1.http://festival.1september.ru/articles/503869/
2.http://www.webmath.ru/poleznoe/formules_19_1.php
3.Л.С.Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Э.Г. Позняк, И.И. Юдина. Геометрия 7-9. Учебник для 7-9 классов средней школы. М.: Просвещение, 2004.
4.http://100formul.ru/55
5.http://mschool.kubsu.ru/cdo/shabitur/kniga/geometr/6_3/6_3.html
6.https://www.youtube.com/watch?v=529Rj_xaS9Q
Литвинова Александра