Решение логических функций в Wolfram|Alpha

WolframAlpha предоставляет бесплатный и неограниченный доступ к своей базе знаний, которая включает огромное количество сведений о нашем мире в числовом измерении. Демография, экономика, история, лингвистика, физика, биология, химия…, и конечно же МАТЕМАТИКА — математические правила, формулы, алгоритмы — здесь есть все это, и многое-многое другое. 

Для студентов, изучающих математику, WolframAlpha настоящая находка. Этот веб-сервис легко решает уравнения и системы, строит графики функций, вычисляет пределы, находит производные, берет интегралы…

Логическая функция — это функция, в которой переменные принимают только два значения: логическая единица или логический ноль. Истинность или ложность сложных суждений представляет собой функцию истинности или ложности простых. Эту функцию называют булевой функцией суждений f(A, B).
Запишим в виде логической функции следующее высказывание:

 Если Иванов здоров и богат, то он здоров.

Решение:

1.Нам дано сложное составное высказывание. Выделим из него простые высказывания:

А = «Иванов здоров»

В = «Иванов богат»

Запишем высказывание в виде логической функции f(A, B)=A/\B=>A

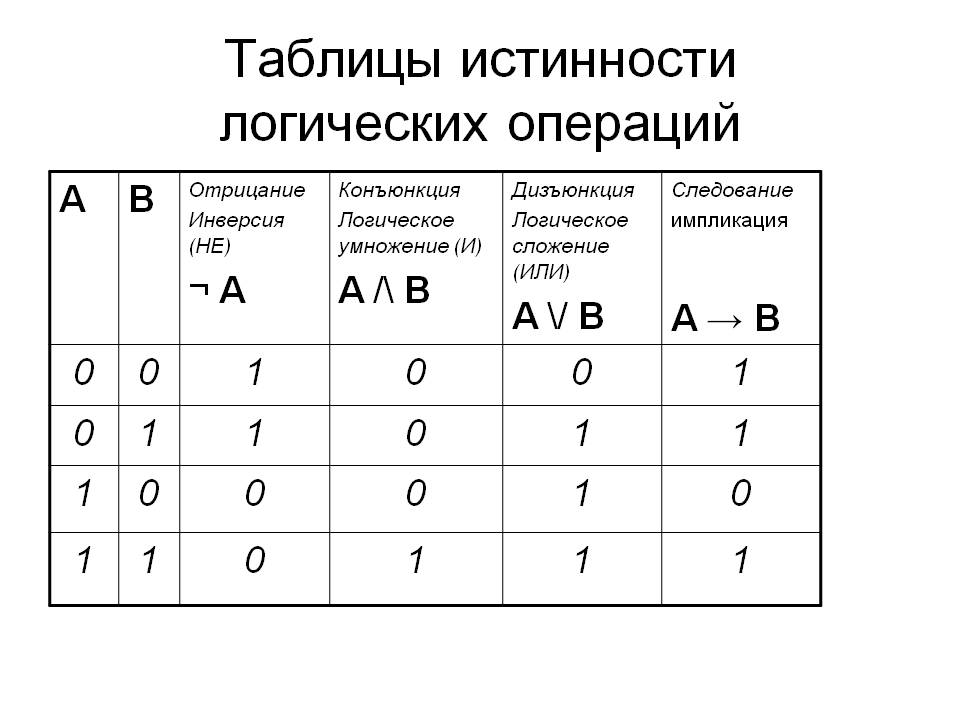
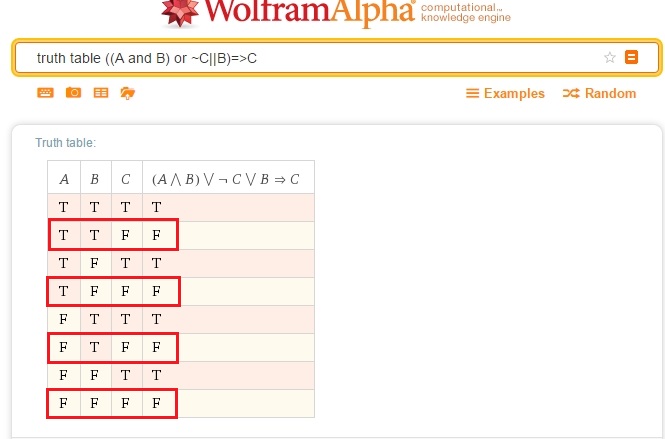
Любая логическая функция может быть задана с помощью таблицы истинности, в левой части которой записывается набор аргументов, а в правой части — соответствующие значения логической функции.

Построение таблицы истинности является для Wolfram|Alpha элементарной задачей.

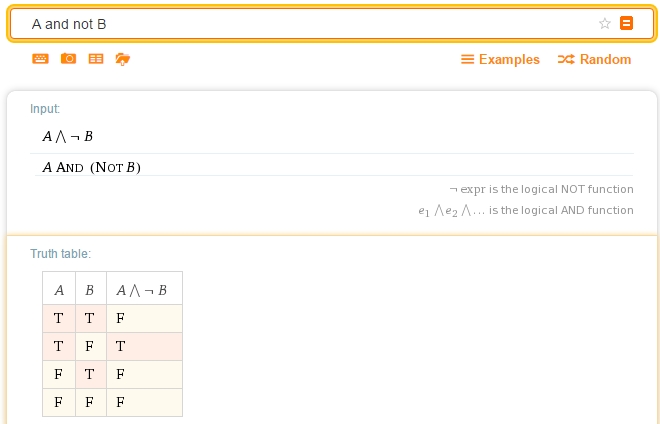
Рассмотрим простой пример: A and not B

T(true)=1

F(false)=0

В ответ на ввод логической функции, Wolfram|Alpha выводит не только таблицу истинности, но и другие сведения. Например, графическое представление данной логической функции с помощью диаграммы Венна:

 

Сама таблица истинности выводится по запросу truth table:

 

Задача:

При каких  значениях А, В и С высказывание ((A and B) or ~C||B)=>C ложно?

Рассмотренные ранее задачи это только самая малая часть того, что Wolfram Alpha может сделать…