Сечение многогранников (10-й класс)

1) Если две точки прямой лежат в некоторой плоскости, то и вся прямая лежит в данной плоскости;

2) Если две плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.

Теорема: если две параллельные плоскости пересечены третьей плоскостью, то прямые пересечения параллельны.

Сечение – это изображение фигуры, которая получается при мысленном рассечении тела плоскостью.

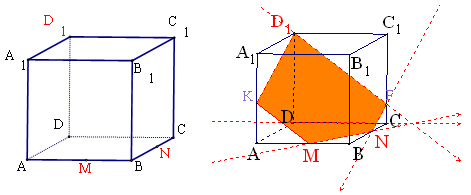
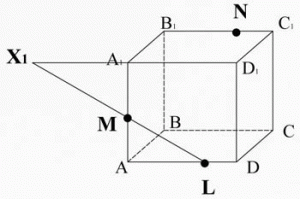
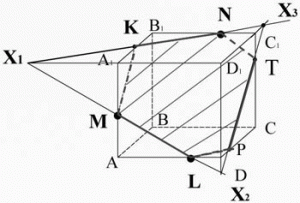
Ребята, перед вами пример неправильного построения сечения куба АС1 плоскостью, проходящей через заданные точки N, C, D1.

А рядом сечение построено верно.

Рассмотрим пример.
Построить сечение куба, проходящее через точки М, N, L.

MKNTPL-искомое сечение

Задания группам построить сечение