Двоичная система счисления — позиционная система счисления с основанием 2. Для записи чисел в двоичной системе счисления используются только две цифры: 0 и 1.
Для перевода двоичных чисел в десятичную систему счисления: необходимо вычислить сумму степеней двойки, соответствующих единицам в свёрнутой форме записи двоичного числа
Переведите числа из двоичной системы счисления в десятичную:
Для перевода целого десятичного числа в двоичную систему счисления: нужно последовательно выполнять деление данного числа и получаемых частных на 2 до тех пор, пока не получим частное, равное нулю. Исходное число в двоичной системе счисления составляется последовательной записью полученных остатков, начиная с последнего.
Переведите десятичные числа в двоичные:
Восьмеричная система счисления — позиционная система счисления с основанием 8. Для записи чисел в восьмеричной системе счисление используются цифры: 0, 1, 2, 3, 4, 5, 6, 7.
Для перевода целого восьмеричного числа в десятичную систему счисления следует перейти к его развернутой записи и вычислить значение получившегося выражения.
Переведите восьмеричные числа в десятичную систему счисления
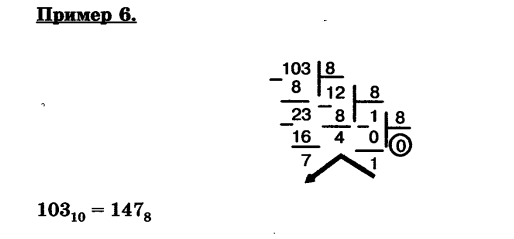
Для перевода целого десятичного числа в восьмеричную систему счисления следует последовательно выполнять деление данного числа и получаемых целых частных на 8 до тех пор, пока не получим частное, равное нулю.
Переведите десятичные числа в восьмеричные:
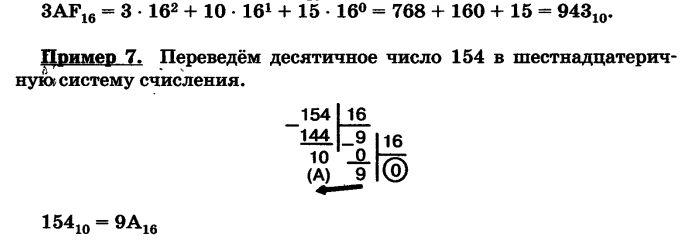
Шестнадцатеричная система счисления — позиционная система счисления с основанием 16. Для записи чисел в восьмеричной системе счисление используются: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
Перевод чисел из одной системы счисления в другую осуществляется аналогично переводу в восьмеричной системе счисления.
Таким образом запись 3AF16 означает:
Переведите десятичные числа в шестнадцатеричные:
Предлагаем выполнить задание для лучшего усвоения материала по теме урока.
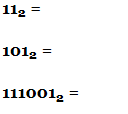
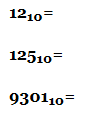
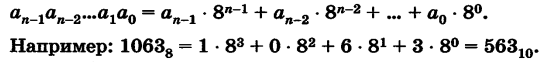
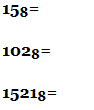
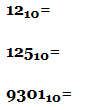
Семён Цветков