Трактовка теоремы

Теорема: В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

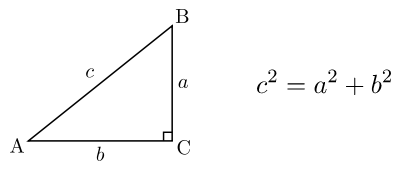
с — гипотенуза(сторона, лежащая напротив прямого угла)
а и b — катеты(стороны, прилегающие к прямому углу)

Доказательство

Пусть треугольник 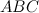 — прямоугольный треугольник с прямым углом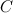 

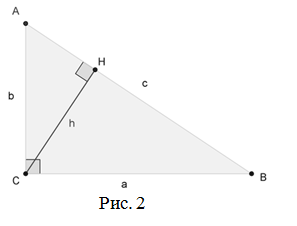
Проведём высоту из вершины 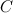 на гипотенузу , основание высоты обозначим как  .

Прямоугольный треугольник 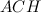 подобен треугольнику  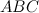по двум углам ( 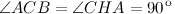, 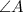— общий). Аналогично, треугольник  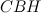подобен  .

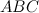Доказательство

Введя обозначения

из подобия треугольников получаем, что

Отсюда имеем, что

Сложив полученные равенства, получаем:

Пифагоровы тройки

В следствии из теоремы Пифагора появились так называемые Пифагоровы тройки.

Пифагорова тройка — упорядоченный набор из трёх натуральных чисел удовлетворяющих квадратному уравнению теоремы Пифагора: При этом числа, образующие пифагорову тройку, называются пифагоровыми числами.

Самая первая пифагорова тройка — 3, 4 и 5. Чем же они интересны?

Интересны они тем, что, например, если вам дается прямоугольный треугольник с катетами 3 и 4, вы сразу можете сказать, что гипотенуза будет равна 5.