Функция y= f(x) называется периодической с периодом Т, если существует число Т, отличное от нуля, такое, что при любом целом n выполняется равенство для любого х принадлежащего D(f): f(x+Tn)=f(x)
Графиком функции y = f(x) называется множество всех точек, у которых абсциссы принадлежат области определения функции, а ординаты равны соответствующим значениям функции.
Другими словами, график функции y = f (х) — это множество всех точек плоскости, координаты х, у которых удовлетворяют соотношению y = f(x).
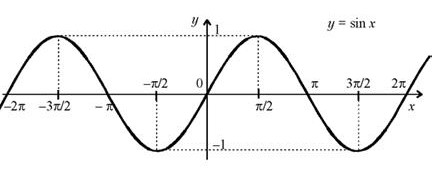
Свойства функции у= sin x:
а) Область определения: D (sin x) = R .
б) Множество значений: E (sin x) = [ – 1 , 1 ] .
в) Четность, нечетность: функция нечетная.
г) Периодичность: функция периодическая с основным периодом T = 2
.
д) Нули функции: sin x = 0 при x = 
n, n 
Z.
е) Промежутки знакопостоянства:
; 
.
ж) Промежутки монотонности:
;
.
з) Экстремумы:
; 
.
График функции y= sin x изображен на рисунке.
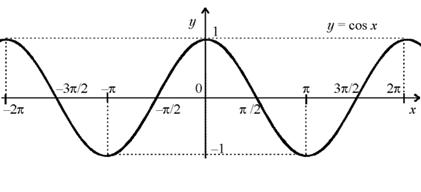
Свойства функции y= cos x:
1) Область определения: D (cos x) = R .
б) Множество значений: E (cos x ) = [ – 1 , 1 ] .
в) Четность, нечетность: функция четная.
г) Периодичность: функция периодическая с основным периодом T = 2
.
д) Нули функции: cos x = 0 при x = 
+ 
n, n 
Z.
е) Промежутки знакопостоянства:
;
.
. ж) Промежутки монотонности:
;
.
з) Экстремумы:
; 
.
График функции y= cos x изображен на рисунке.
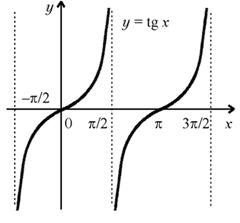
Свойства функции y= tg x:
а) Область определения: D (tg x) = R \ {
/2 + 
n( n 
Z ) }.
б) Множество значений: E (tg x ) = R .
в) Четность, нечетность: функция нечетная.
г) Периодичность: функция периодическая с основным периодом T = 
.
д) Нули функции: tg x = 0 при x = 
n, n 
Z.
е) Промежутки знакопостоянства:
; 
.
ж) Промежутки монотонности: функция возрастает на каждом интервале, целиком принадлежащем ее области определения.
з) Экстремумы: нет.
График функции y = tg x изображен на рисунке.
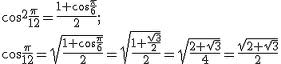
Дмитрий Миронов