Урок №7. Окружность описанная около треугольника.

Вопросы:

1. Что такое серединный перпендикуляр?

2. Свойство точек серединного перпендикуляра.

Прямую, проходящую через середину отрезка перпендикулярно к нему, называют серединным перпендикуляром к отрезку.

Теорема серединных перпендикуляров треугольника.

Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Верно и обратное утверждение: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.

Доказательство.

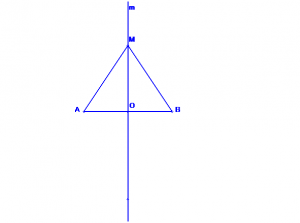
Пусть прямая m — серединный пер­пендикуляр к отрезку АВ, точка О — середина отрезка.

1.Рассмотрим произвольную точку М прямой m и докажем, что АМ = ВМ.

Если точка М совпадает с точкой О, то это равенство верно, так как О — середина отрезка АВ.

Пусть М и О — различные точки.

Прямоугольные треугольники ОАМ и ОВМ равны по двум катетам (ОА = ОВ, ОМ — общий катет), поэтому АМ=ВМ.

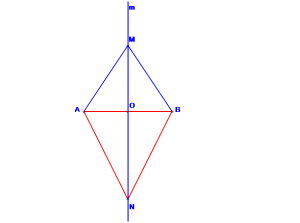
2.  Рассмотрим произвольную точку N, равноудаленную от концов отрезка АВ, и докажем, что точка N лежит на прямой m.

Если N — точка прямой АВ, то она совпадает с середи­ной О отрезка АВ и потому лежит на прямой m.

Если точка N не лежит на прямой АВ, то рассмотрим треугольник ANB, ко­торый равнобедренный, так как AN = BN.

Отре­зок N0 — медиана этого треугольника, а, следовательно, и вы­сота. Таким образом, NO L AB, поэтому прямые ON и m совпада­ют, и, значит,    N — точка прямой m.

Теорема доказана.

Следствие.

 Серединные перпендикуляры к сторонам тре­угольника пересекаются в одной точке.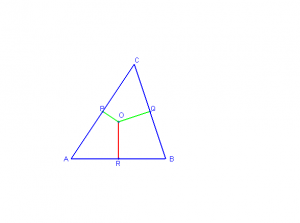

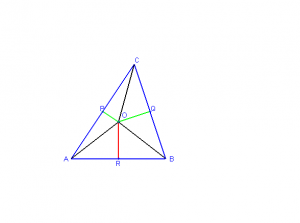
В самом деле, обозначим буквой О точку пересечения сере­динных перпендикуляров OP и OQ к сторонам АC и СB треугольника АВС .

По доказанной теореме ОC =ОА и ОC  = ОB.

Поэтому ОB= ОA, т. е. точка О равноудалена от концов отрезка АB и, значит, лежит на серединном перпендикуляре OR  к этому отрезку.

Следовательно, все три серединных перпен­дикуляра  OP, OQ и OR к сторонам треугольника АВС пересекаются в точке О.

ОКРУЖНОСТЬ ОПИСАННАЯ ОКОЛО ТРЕУГОЛЬНИКА.

Если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник — вписанным в эту окружность.

Вопросы:

1. Где находятся точки равноудалённые от концов отрезков?

2. Где находится центр  окружности описанной около треугольника?

Теорема. Около любого треугольника можно описать окружность.

Доказательство.

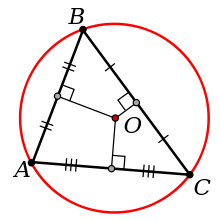
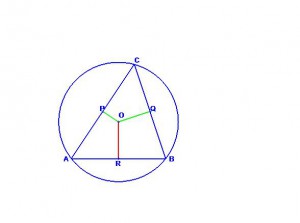
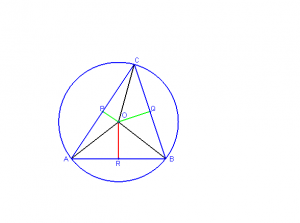
Рассмотрим произвольный треугольник АВС .

Обозначим буквой O точку пересечения серединных перпендикуляров к его сторонам и проведём отрезки OA, OB и OC.

Так как точка O равноудалена от вершин , то , следовательно,  окружность с центром в точке O радиуса OA проходит через все три вершины треугольника , следовательно, является описанной около треугольника АВС.

.

Окружность называется описанной около треугольника, если она проходит через все его вершины.

Замечание. Отметим, что около треугольника можно описать только одну окружность. В самом деле, допустим, что около треугольника можно описать две окружности. Тогда центр каждой окружности равноудален от вершин треугольника и, значит, совпадает с точкой О пересечения серединных перпендикуляров к сторонам треугольника, а радиус равен расстоянию от точки О до вершин треугольника. Следовательно, эти окружности совпадают.

Вопрос:

1.Какие теоремы нужно вспомнить когда мы говорим о описанной окружности?

Это интересно:

Центр окружности, которую описала радуга, всегда лежит на прямой, проходящей через солнце и глаз наблюдателя.