Основатель проекта, Стивен Вольфрам.
Wolfram|Alpha не возвращает перечень ссылок, основанный на результатах запроса, а вычисляет ответ, основываясь на собственной базе знаний, которая содержит данные о математике, физике, астрономии, химии, биологии, медицине, истории, географии, политике, музыке, кинематографии, а также информацию об известных людях и интернет-сайтах. Он способен переводить данные между различными единицами измерения, системами счисления, подбирать общую формулу последовательности, находить возможные замкнутые формы для приближенных дробных чисел, вычислять суммы, пределы, интегралы, решать уравнения и системы уравнений, производить операции с матрицами, определять свойства чисел и геометрических фигур. Однако, расчет на основании собственной базы имеет и свои недостатки, в том числе — уязвимость к ошибкам данных.
Внешний вид:
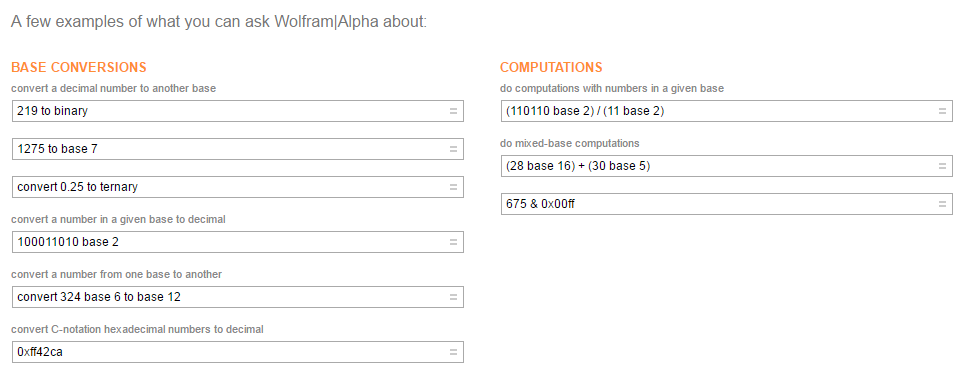
На стартовой странице представлена удобная сортировка по категориям. При выборе категории можно сразу посмотреть примеры.
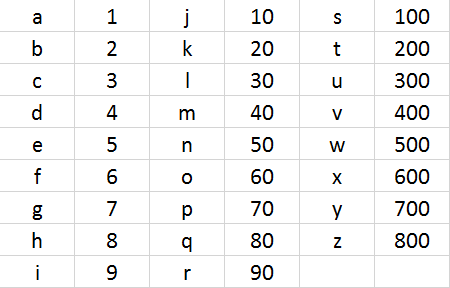
На одном из уроков мы с Вами рассматривали основы криптографии и простейшие шифры. На самом деле, для шифровки информации можно использовать и перевод чисел в различные системы счисления. Переводить можно и буквы, предварительно присвоив им числовые идентификаторы. Напоминание: в русском алфавите — 33 буквы, в английском — 26. Соответственно, если рассматривать английский алфавит (более распространен), то a — 1, … , z — 26. Получается таблица:
Разумеется, мы не можем закодировать точку, пробел и заглавные буквы в силу несовершенства таблицы соответствия, что в данной задаче не критично. Множественная интерпретация исключена.
Итак: 85303060 5006090304. 9200 9100 14018009507.
На самом деле, даже такая запись является шифром, но все еще очень слабым. Поэтому предлагаю воспользоваться знаниями о системах счисления и усложнить задачу расшифровки потенциальному недоброжелателю.
Небольшое напоминание:
Для перевода из десятичной системы счисления в систему с основанием k необходимо производить деление исходного числа на k, запоминая остатки от деления и продолжая данную операцию с целочисленным значением деления до тех пор, пока результатом деления не будет ноль. Искомым представлением числа будет запись, составленная из полученных остатков от деления, записанных в обратном порядке. Ниже представлены примеры перевода в двоичную и шестнадцатеричную систему счисления:
Для того, чтобы представить какое либо число в десятичной системе счисления, следует вычислить сумму всех цифр данного числа, умноженных на порядок системы счисления, возведенной в степень, равную номеру разряда данной цифры. Следующие примеры демонстрируют суть данного метода:
hello = 5159f14
world = 12a62e040
it = 23f0
is = 238c
amazing = 34389d9a3
hello = 817607328005802600
world = 47982055007278710000
it = 88179573132000
is = 87221099511000
amazing = 134358923313867100000
Получившийся шифр можно расшифровать только с помощью симметричного ключа: 9584736210.
Конечно, представленный шифр является неудобным из-за своей громоздкости, однако, его довольно сложно взломать.
Также мы с вами познакомились с системой WolframAlpha, в частности с разделом преобразований в различные системы счисления.
Самостоятельная работа:
На основе вышеизложенного попробуйте придумать свой алгоритм шифрования на основе систем счисления. Докажите его криптостойкость. Использование системы WlframAlpha приветствуется.




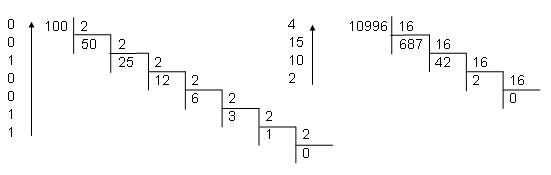







Жданович Дмитрий