Геометрия -одна из наиболее древних наук. Первые геометрические факты найдены в вавилонских клинописных таблицах и египетских папирусах (III тысячелетие до нашей эры), а также в других источниках. Название науки «геометрия» древнегреческого происхождения, оно составлено из двух древнегреческих слов: «ge» — «земля» и «metreo» — «измеряю» (землю измеряю).


geometr
Геометрия—это раздел математики, изучающий геометрические фигуры и их свойства.
Точка — это основная и самая простая геометрическая фигура.
Прямая — это самая простая геометрическая фигура, которая не имеет ни начала, ни конца.(Слова «не имеет ни начала, ни конца» говорят о том, что прямая бесконечна.)
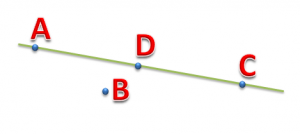
1. Начертите прямую. Как ее можно обозначить?
2. Отметьте точку С, не лежащую на данной прямой, и точки D, Е, К, лежащие на этой же прямой.
Символы принадлежности
принадлежит не принадлежит
3. Используя символы принадлежности, запишите предложение «Точка D принадлежит прямой АВ, а точка С не принадлежит прямой а».
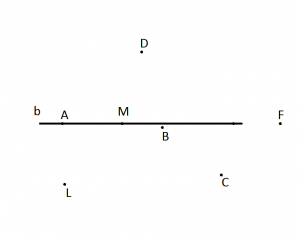
4. Используя рисунок и символы принадлежности, запишите, какие точки принадлежат прямой b, а какие — нет.
— Сколько прямых можно провести через заданную точку А?
— Сколько прямых можно провести через две точки?
-Через любые две точки можно провести прямую?
Итак, через любые две точки можно провести прямую и притом только одну.
Это утверждение назовем свойством прямой.
5.Начертите прямые XY и MK, пересекающиеся в точке О.
Для того, чтобы кратко записать, что прямые XY и MK пересекаются в точке О, используют символ ∩ и записывают так: XY ∩ MK = О.
— Сколько общих точек может быть у двух прямых?
6. На прямой а отметьте последовательно точки А, В, С, D. Запишите все получившиеся отрезки.
7. Начертите прямые а и b, пересекающиеся в точке М. На прямой а отметьте точку N, отличную от точки М.
а) Являются ли прямые MN и а различными прямыми?
б) Может ли прямая b проходить через точку N?
Решить задачи:
1) Сколько точек пересечения могут иметь три прямые? Рассмотрите все возможные случаи и сделайте соответствующие рисунки.
2) На плоскости даны три точки. Сколько прямых можно провести через эти точки так, чтобы на каждой прямой лежали хотя бы две из данных точек? Рассмотрите все возможные случаи и сделайте рисунки.
Домашнее задание
1.§ 1,2, вопросы 1-3
2. Решить задачи.
№1-4 из рабочей тетради;
№ 1, 3, 4, 7. — учебник















Ирина Юрьевна Мурадова