Равнобедренный треугольник
Треугольник называется равнобедренным, если две его стороны равны.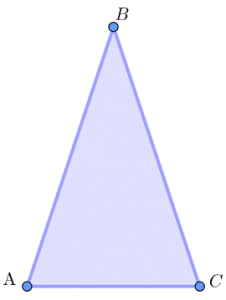
АВ, АВ, ВС — боковые стороны равнобедренного треугольника
А, С – углы при основании равнобедренного треугольника
АС — основание равнобедренного треугольника
В – угол при вершине равнобедренного треугольника
◊ Теорема 1. В равнобедренном треугольнике углы при основании равны
Дано: Δ АВС – равнобедренный, АС – основание
Доказать: ∠А = ∠С
◊ Теорема 2. В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой
Дано: Δ АВС –равнобедренный, АС – основание, ВD – биссектриса.
Доказать: 1. ВD – медиана 2. ВD – высота
1. Высота равнобедренного треугольника, проведённая к основанию, является медианой и биссектрисой. 2. Медиана равнобедренного треугольника, проведённая к основанию, является высотой и биссектрисой.
◊ Задача.
В равнобедренном треугольнике ABC
проведена биссектриса AD к основанию.
Отрезок BD равен 7 см.
Найдите основание
треугольника.
Ссылки на используемые ресурсы
- https://ege-ok.ru/wp-content/uploads/2014/01/59_2-Geometriya.-7-9-kl.-Uchebnik_Atanasyan-L.S.-i-dr_2010-384s.pdf
- https://budu5.com/manual/chapter/3320
- https://ppt-online.org/204148












Наталья Фрикель