Деление – это арифметическое действие обратное умножению, посредством которого узнаётся, сколько раз одно число содержится в другом.
Повторяя операцию вычитания 2 из 10, мы находим, что 2 содержится в числе 10 пять раз. Это легко проверить сложив пять раз 2 или умножив 2 на 5:
Деление обозначается знаком : (двоеточие), ÷ (обелюс) или / (косой чертой) и читается: разделить на. Знак деления ставится между делимым и делителем. Делимое записывается слева от знака деления, а делитель – справа:

Также деление можно рассматривать как действие, посредством которого одно число делится на столько равных частей, сколько единиц содержится в другом числе (на которое делится). Таким образом определяется сколько единиц содержится в каждой отдельной части.
Например, у нас есть 10 яблок, разделив 10 на 2 мы получим две равные части, каждая из которых содержит 5 яблок:
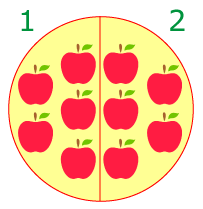
Для проверки деления можно частное умножить на делитель (или наоборот). Если в результате умножения получится число, равное делимому, то деление сделано верно:
12 : 4 = 3
Теперь выполним проверку деления:
3 · 4 = 12
Делить на нуль нельзя.
Рассмотрим, почему нельзя делить на нуль. Если делимое не нуль, а любое другое число, например 4, то разделить его на нуль значило бы найти такое число, которое после умножения на нуль даёт в результате число 4. Но такого числа нет, потому что любое число после умножения на нуль даёт снова нуль.
Если же делимое тоже равно нулю, то деление возможно, но частным может служить любое число, потому что в этом случае любое число после умножения на делитель (0) даёт нам делимое (т. е. снова 0). Таким образом, деление хоть и возможно, но не приводит к единственному определённому результату.



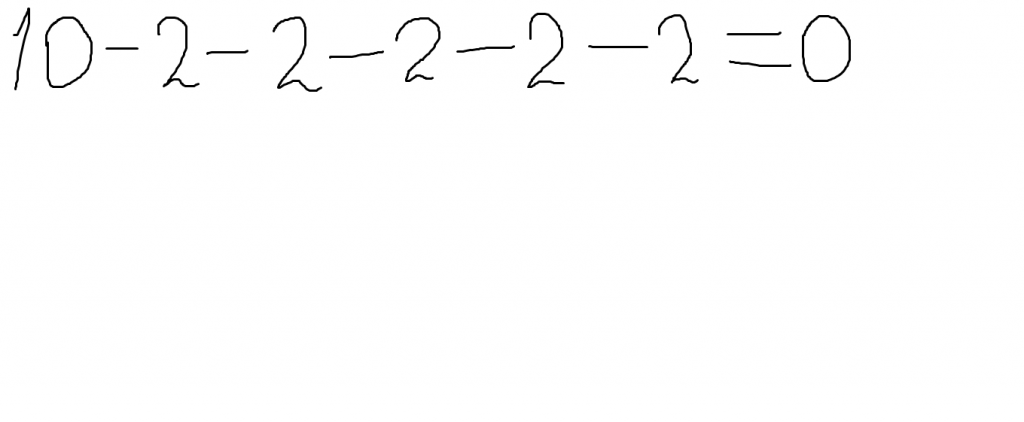
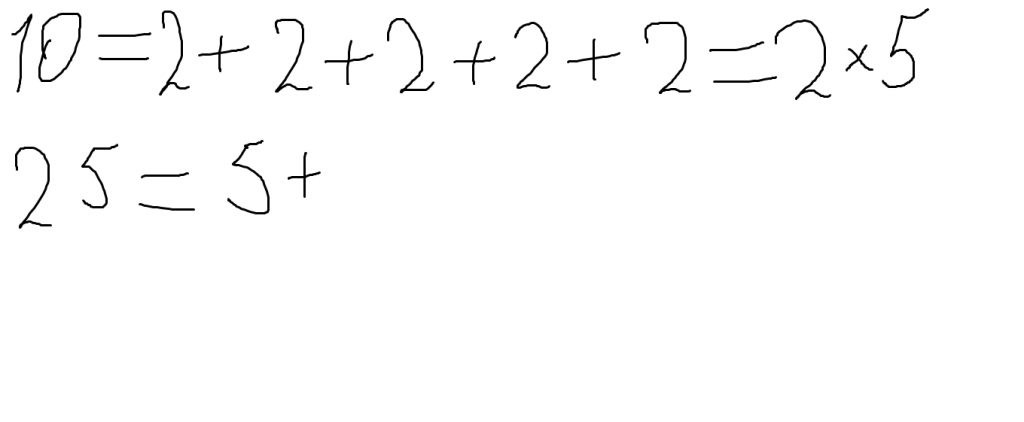
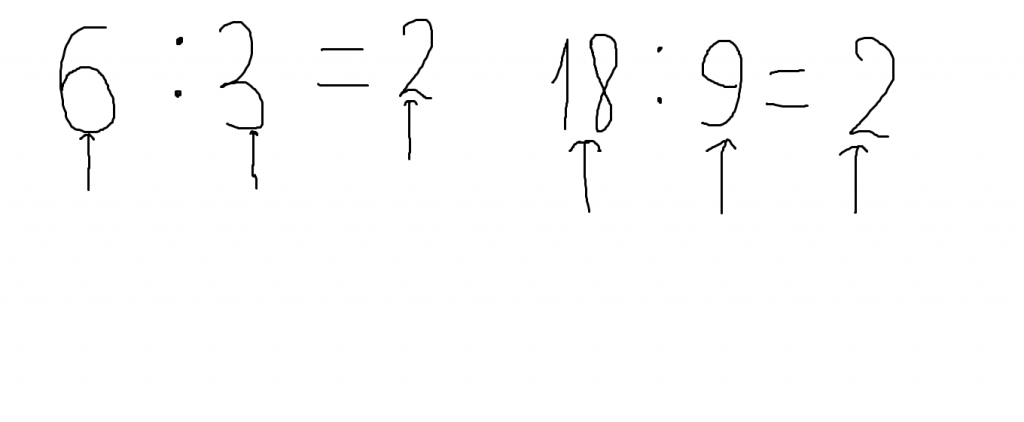
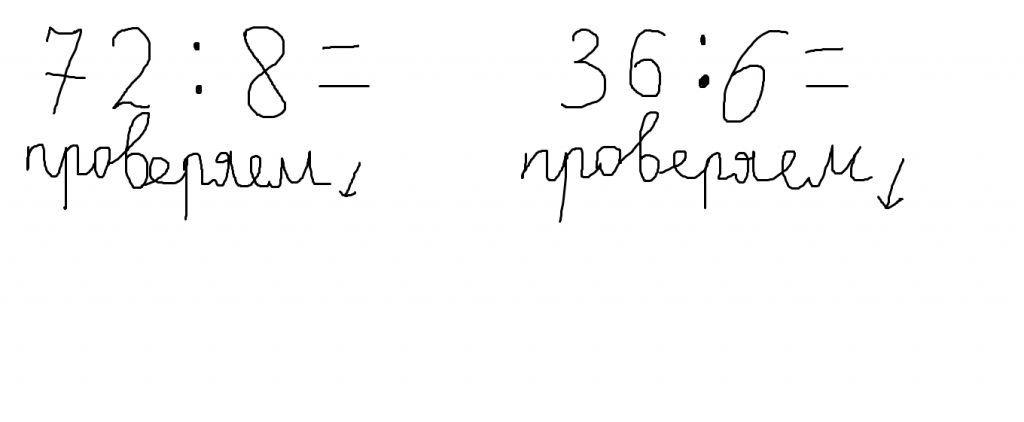










Шамин Николай