О чем речь?

Ей было тысяча сто лет,
Она в сто первый класс ходила,
В портфеле по сто книг носила –
Все это правда, а не бред.
Когда, пыля десятком ног,
Она шагала по дороге,
За ней всегда бежал щенок
С одним хвостом, зато стоногий.
Она ловила каждый звук
Своими десятью ушами,
И десять загорелых рук
Портфель и поводок держали.
И десять темно-синих глаз
Рассматривали мир привычно,
Но станет все совсем обычным,
Когда поймете наш рассказ.

Системы счисления

Перевод чисел

Каждое число в позиционной системе счисления можно представить в виде суммы произведений коэффициентов на степени основания системы счисления.

(степени расставляем над целой частью числа слева направо, начиная с «0»)

Теперь рассмотрим алгоритм перевода чисел из произвольной системы счисления в десятичную.

Перевод чисел из произвольной системы счисления в десятичную:

(степени расставляем над целой частью числа слева направо, над дробной частью – справа налево, начиная с «-1»)

Двоичная система счисления имеет особую значимость в информатике. Это определяется тем, что внутреннее представление любой информации в компьютере является двоичным, т.е. описываемым наборами только из двух знаков (0, 1).

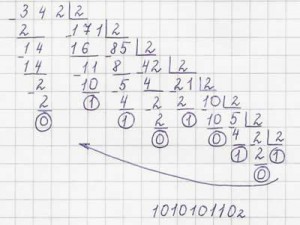
Рассмотрим пример перевода числа из десятичной системы счисления в двоичную:

Результатом является число, составленное из остатков от деления на 2 (которые мы обводили в кружок), записанное справа налево.

342₁₀ = 101010110₂

Алгоритм перевода чисел

Теперь попробуйте записать рассмотренный алгоритм перевода числа из десятичной системы счисления словами.

Порешаем…

Перевести в десятичную систему счисления числа:

101111001₂                    1231₃                        110110101₂                          1223₃

Перевести из десятичной системы счисления в двоичную, и наоборот числа:

256                                457                              845                              1073

Записать алгоритм перевода числа из десятичной системы счисления в произвольную систему счисления.

Поиграем…

Подведем итоги

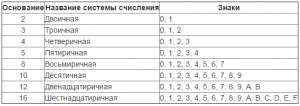
Что такое система счисления

Дайте определение понятию «основание системы счисления»

Как перевести число из десятичной системы счисления в двоичную (алгоритм)

Так что написано в стихотворении?

Домашнее задание

Источник:

http://festival.1september.ru/articles/573575/