сакен
пнrrr
Серединный перпендикуляр (срединный перпендикуляр или медиатриса) — прямая, перепендикулярная к данному отрезку и делящая его на две равные части.
Выясним, каким геометрическим местом точек является серединный перпендикуляр.
Теорема. Серединный перпендикуляр к отрезку является геометрическим местом точек, одинаково удаленных от концов этого отрезка.
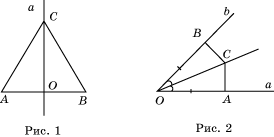
Доказательство. Пусть дан отрезок АВ и точка О – его середина. Покажем, что геометрическим местом точек, одинаково удаленных от точек А и В является серединный перпендикуляр к отрезку АВ (рис. 1). Действительно, очевидно, точка О одинаково удалена от точек А, В и принадлежит серединному перпендикуляру. Если точка С одинаково удалена от точек А и В и не совпадает с точкой О, то треугольник АВС равнобедренный и СО – медиана. По свойству равнобедренного треугольника медиана является также и высотой. Значит, точка С принадлежит серединному перпендикуляру. Обратно, пусть точка С принадлежит серединному перпендикуляру и не совпадает с О, тогда прямоугольные треугольники АОС и ВОС равны (по катетам). Следовательно, АС=ВС.
Задание 1:
Пусть АВ — данный отрезок. Построим две окружности с центрами в точках А и В радиуса АВ . Эти окружности пересекаются в двух точках C и D. Отрезки AC, АD, BC, ВD равны друг другу как радиусы этих окружностей.
Проведем прямую CD. Она является искомым серединным перпендикуляром к отрезку АВ. В самом деле, точки C и D равноудалены от концов отрезка АВ, поэтому они лежат на серединном перпендикуляре к этому отрезку. Значит, прямая CD и есть серединный перпендикуляр к отрезку АВ.
ИЛИ ???
Задание 1:
Восставить серединный перпендикуляр через данный отрезок и точку, не лежащую на нем .
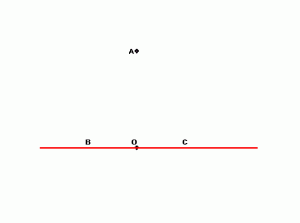
На прямой даны две точки с координатами А(-1;0) и В(1;0) и точка, не лежащая на этой прямой, с координатами С(0;1).
Ход построения:
1. Провести прямую, отметить на ней точки А и В.
2. Поставить точку С, не принадлежащую этому отрезку.
3. Проведем полуокружность, с центром в точке А радиусом, равным 2,проходящую через точку С.
4. Проведем такую же полуокружность, с центром в точке В радиусом, равным 2, проходящую через точку С.
5. Получим точки пересечения С и D этих полуокружностей.
5.Провести прямую, проходящую через точки С и D.
Т.о. мы получаем серединный перпендикуляр, проходящий через точки С и D, и пересекающий отрезок АВ в точке Р.
Задание 2:
Восставить серединный перпендикуляр через данный отрезок и точку не лежащую на нем.
На прямой даны две точки с координатами В(-6;0) и С(6;0) и точка, не лежащая на этой прямой, с координатами А(1;2).
Ход построения:
1. Провести прямую, отметить на ней точки В и С.
2. Поставить точку А, не принадлежащую этому отрезку.
3. Проведем полуокружность, проходящую через точки В и С (АВ — диаметр этой полуокружности).
4. Находим середину этого отрезка АВ, точку О.
5. Проведем прямую, проходящую, через точки А и О.
Т.о. мы получаем серединный перпендикуляр, проходящий через точки А и О.
Задание 3:
Восставить серединный перпендикуляр через данный отрезок и точку не лежащую на нем.
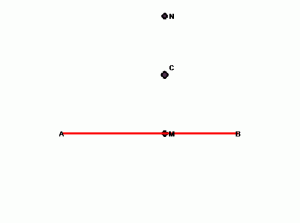
На прямой даны две точки с координатами А(-6;0) и В(6;0) и точка, не лежащая на этой прямой, с координатами С(1;4).
Ход построения:
1. Провести прямую, отметить на ней точки А и В.
2. Поставить точку С, не принадлежащую этому отрезку.
3. Проводим прямую, перпендикулярную отрезку АВ через точку С.
4. Получим отрезок СМ.
5. На прямой откладываем отрезок СN, равный длине отрезка СМ.
6. Проведем окружность, с центром в точке С.
Т.о. мы получаем серединный перпендикуляр, проходящий через точки N и М.
Задание 4: НЕ СОВСЕМ ПОЛУЧАЕТСЯ!!!
Построение касательной из точки на(вне) окружности
Понятие касательной появилось еще в древности. Построение этих прямых сначала к окружности, а потом к эллипсам, параболам и гиперболам с помощью линейки и циркуля проводилось еще на начальных этапах развития геометрии.
Определение: Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности.
Задание: Построить касательную к данной окружности, проходящую через заданную точку, лежащую вне этой окружности.
Решение: Дана окружность с центром в точке А и точка В вне этой окружности. Постоим отрезок АВ. Около отрезка АВ, как около диаметра, опишем окружность, точки пересечения полученной окружности с данной и будут точками касания прямых.
Пояснение:(по теореме)Если радиус перпендикулярен прямой в точке пересечения ею окружности, то эта прямая — касательная к этой окружности.
Задание: Построить касательную к данной окружности, проходящую через заданную точку, лежащую на этой окружности.
Решение: Дана окружность с центром в точке А и точка В на этой окружности. Постоим отрезок ВС равный отрезку АВ. Около т. С опишем окружность, радиуса больше отрезка ВС. Аналогично, построим окружность с центром в т. А, с тем же радиусом.Через точки пересечения данных окружностей (т. Р и т.Q) проведем прямую PQ. Полученная прямая будет касательной к окружности, а т.В будет точкой касания прямой.
Пояснение:(по теореме)Прямая, перпендикулярная к радиусу в конечной его точке, лежащей на окружности, является касательной к окружности.
В школьном курсе рассматривают два вида преобразований плоскости: движения и преобразования подобия (гомотетию), которые являются линейными преобразованиями, то есть такими, при которых прямые переходят в прямые. Однако, существуют и нелинейные преобразования, при которых, например, прямая может перейти в какую-либо кривую. Рассмотрим с вами такое преобразование плоскости, при котором прямые переходят в известную нам кривую — окружность. Это замечательное преобразование называется инверсией.
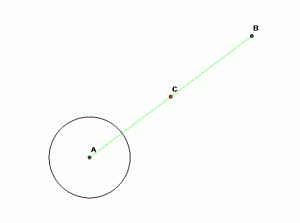
Инверсия относительно окружности с центром O и радиусом R – это преобразование, которое каждой точке А ставит в соответствие точку В, лежащую на луче OА так, что OA · OВ = R·R
Точку О называют началом или центром инверсии, про точки А и В говорят, что они соответственные, а R·R называют степенью инверсии.
Из определения следует, что:
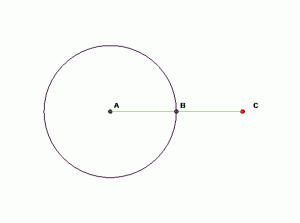
- для каждой точки плоскости, кроме центра инверсии, существует единственная точка, соответственная данной
- для центра инверсии соответственной точки не существует
- любой точке, лежащей на окружности, соответствует она сама
- если при инверсии точка А перейдет в точку В, то и точка В перейдет в точку А
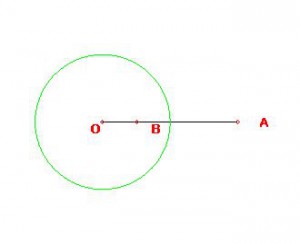
Теперь разберемся, как построить соответственную точку?
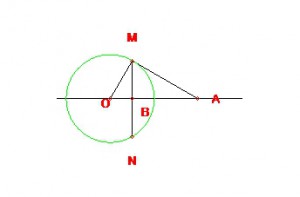
Пусть дана некоторая окружность с центром в точке О (центр инверсии) и точка А, для которой требуется построить соответственную точку. Проведём из точки А касательные к окружности, которые пересекут её в точках M и N. Отрезок MN пересекает прямую ОА в точке В, являющийся соответственной для А.
Верность построения легко показать
Точка В лежит на прямой ОА, поскольку МВ является высотой прямоугольного треугольника ОМА. Из подобия прямоугольных треугольников ОМА и ОВМ следует пропорция
OM / OB = OA / OM, или ОА · ОВ = ОМ·ОМ.
Если же точка А находиться внутри окружности, то построения соответственной точки В ведется в обратном порядке: сначала строим перпендикуляр к ОА, проходящий через точку А, до пересечения с окружностью, потом строим касательную, которая пересекает ОА в нужной точке.
1. 1 Прямая, проходящая через центр инверсии, при инверсии переходит в себя.
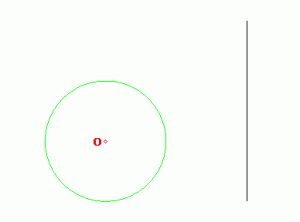
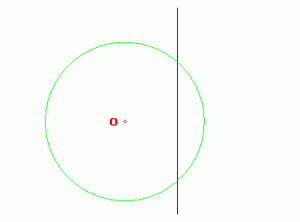
1.2 Прямая, не проходящая через центр инверсии, при инверсии переходит в окружность, проходящую через центр инверсии.
(расстояние до прямой > R) (расстояние до прямой < R)
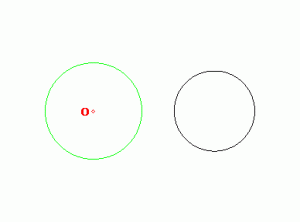
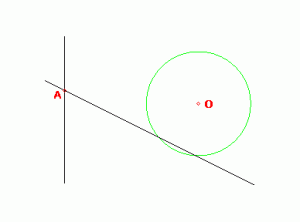
2.1 Окружность, проходящая через центр инверсии, при инверсии переходит в прямую (обратно 1.2).
2.2 Окружность, не проходящая через центр инверсии, при инверсии переходит в окружность.
3. Инверсия является конформным преобразованием, т.е. сохраняет углы в точках пересечения кривых. Если углы рассматривать как ориентированные, то ориентация углов при инверсии изменяется на противоположную.
Для черчения обратных кривых можно использовать особый прибор инверсор (смотрите для примера инверсор Поселье и Липкина). С помощью инверсии можно изящно решить задачи Аполлония, Мальфатти, Архимеда и Паппа, показать, что все построения, которые можно сделать с помощью циркуля и линейки, можно сделать с помощью одного циркуля (прямая считается построенной, если известны две её точки) и многое другое.
Окружность Аполлония
Окружность Аполло́ния — геометрическое место точек плоскости, отношение расстояний от которых до двух заданных точек — величина постоянная, отличная от нуля и единицы.
Задание: Дан отрезок ВА и точка М, не принадлежащая данному отрезку. Построить окружность Аполлония.
Решение: На луче ВМ от точки М откладываем отрезок длиной равный МА внутренним и внешним образом. Полученные точки Q и C соединяем с точкой A. Проводим из точки М прямые параллельные отрезкам АС и АQ, в результате получаем точку H и N. Затем по теореме Фалеса имеем нужное соотношение. Отрезок HN будет является диаметром окружности Аполлония.
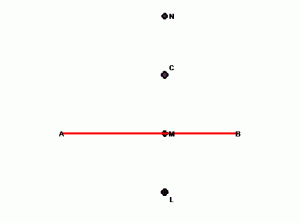
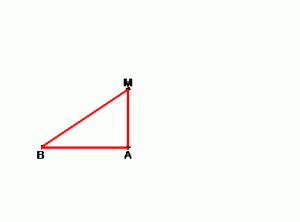
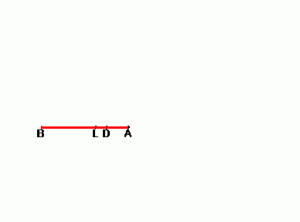
Задача: Дан отрезок ВА и две точки L и D, где L — основание биссектрисы, а D — основание высоты. Построить треугольник.
Ход решения:
- Восстановим перпендикуляр из точки D.
- Проведем прямую проходящую через точку В и не пересекающую луч исходящий из точки D.
- Отложим на этой прямой отрезок BQ=BD.
- На отрезке BQ от точки Q отложим отрезок HQ=LA.
- Проведем прямую через точки H и A.
- Проведем прямую параллельную прямой HA и проходящую через точку Q, она пересекает прямую ВА в точке N.
- Построим окружность с диаметром LN, она пересечет перпендикуляр в точке M.
- Соединим точку М с точками В и А, получим искомый треугольник ВМА.














Шамурадова Гуля