Построение сечений многогранников

Построение сечений многогранников
Построение сечений многогранников

Комплект учебных материалов  по теме «Построение сечений в многогранниках» разработан для использования на уроках геометрии в 10 классе общеобразовательной школы.

Комплект содержит в себе:
— урок для интерактивной доски;
— набор заданий для закрепления ЗУНов.

 

На страницу урока →

 

На этом занятии мы научимся решать задачи на построение сечений тетраэдра и параллелепипеда. Добро пожаловать в мир увлекательной науки геометрии!

 Освежим в памяти те знания, которые нам понадобятся для успешного изучения темы.

 

 

 

Персиковая плоскость является сечением параллелепипеда

Персиковая плоскость является сечением параллелепипеда

 

Секущая плоскость — любая плоскость, по обе стороны от которой имеются точки данной фигуры.

При пересечении секущей плоскости и многогранника получается многоугольник, этот многоугольник   называется сечением многогранника плоскостью.

Сегодня мы научимся строить сечения параллелепипеда и тетраэдра.

Построение сечения тетраэдра.

Задача 1. 
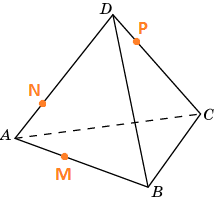
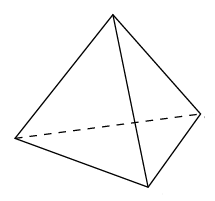
Построить сечение тетраэдра, проходящее через точки M, N, P.

—

55_html_4b408853 2-1

 

Задача 2. 
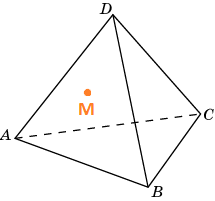
Построить сечение тетраэдра плоскостью, проходящей через точку М и параллельной основанию АВС.

—

55_html_4b408853 2-2

Построение сечения параллелепипеда.

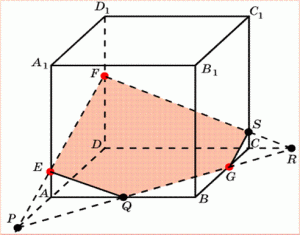
Задача 3.
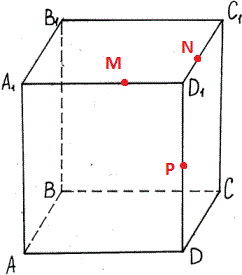
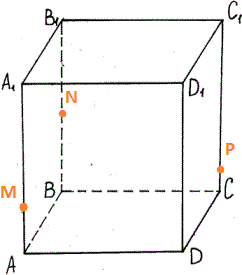
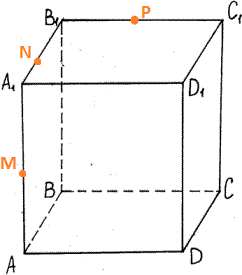
Построить сечение параллелепипеда плоскостью, проходящей через точки M, N, P.

—

parallelegram 2-1

Задача 4.
Построить сечение параллелепипеда плоскостью, проходящей через точки M, N, P.

—

parallelegram 2-2

 

Задача 5.
Построить сечение параллелепипеда плоскостью, проходящей через точки M, N, P.

—

parallelegram 2-3

—

 

А теперь попробуйте свои силы в построении сечений. Задания для самостоятельного выполнения.

Задача: Изобразите тетраэдр DABC и постройте сечение этого тетраэдра плоскостью, проходящей через точку М параллельно плоскости грани АВС, если а) точка М лежит внутри грани ABD;  б) точка М является серединой ребра AD.

—

                        55_html_4b408853                                  55_html_4b408853

Задача: Изобразите параллелепипед ABCDEFGH  и постройте его сечение плоскостями ABG и CDF, а также отрезок, по которому эти плоскости пересекаются.

 

parallelegram

Задача: Изобразите параллелепипед ABCDEFGH и постройте его сечение плоскостью MNK, где точки M, N и K лежат соответственно на ребрах: BF, AE, AD.

—

parallelegram

Дома выполнить на отдельном листке номера: №104 -107, 114, 115,  и сдать на проверку на следующем уроке.

*Учебник: Геометрия. 10-11 классы: учеб. для общеобразоват. учреждений: базовый и профил. уровни / [Л.С. Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др.]. — 18-е изд. -М.:Просвещение, 2009. -255 с.