Квадратное уравнение
это уравнение вида ax2 + bx + c = 0, где x — свободная переменная, a, b, c — коэффициенты, причём a не равно 0.
Приведённым называют квадратное уравнение, в котором старший коэффициент равен единице. Такое уравнение может быть получено делением всего выражения на старший коэффициент a:
x^2 + px + q = 0, \quad p=\frac{b}{a}, \quad q=\frac{c}{a}.
Полным квадратным уравнением называют такое, все коэффициенты которого отличны от нуля.
Неполным квадратным уравнением называется такое, в котором хотя бы один из коэффициентов кроме старшего (либо второй коэффициент, либо свободный член) равен нулю.
Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:
1)Не имеют корней;
2)Имеют ровно один корень;
3)Имеют два различных корня.
В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант.
Дискриминант
Определение: Пусть дано квадратное уравнение ax2 + bx + c = 0. Тогда дискриминант — это просто число D = b2 − 4ac.
Эту формулу надо знать наизусть. По знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:
Если D=0, корней будет два.
Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете: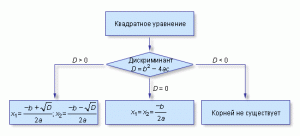
Задача
Сколько корней имеют квадратные уравнения:
x2 − 8x + 12 = 0;
5×2 + 3x + 7 = 0;
x2 − 6x + 9 = 0.
Решение
Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a = 1, b = −8, c = 12;
D = (−8)2 − 4 · 1 · 12 = 64 − 48 = 16
Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a = 5; b = 3; c = 7;
D = 32 − 4 · 5 · 7 = 9 − 140 = −131.
Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a = 1; b = −6; c = 9;
D = (−6)2 − 4 · 1 · 9 = 36 − 36 = 0.
Дискриминант равен нулю — корень будет один.
Ответ
1) 2 корня; 2) нет корней; 3) один корень.
Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове.
Неполные квадратные уравнения
Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:
x2 + 9x = 0;
x2 − 16 = 0.
Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:
Определение: Уравнение ax2 + bx + c = 0 называется
неполным квадратным уравнением,
если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.
Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.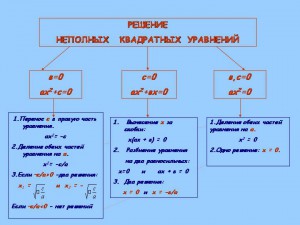
кроссворд
тест
kvadratnye-uravneniya
http://bmanya1108.edu.glogster.com/kwadratnyi-urawnenie/
Алгебра 8 класс А.В. Макарычев
Алгебра 9 класс С.В. Мордкович
Дидактические материалы по алгбере 8 класс В.С. Жохов, А.В. Макарычев












Бирюкова Мария