В отличии от линейных уравнений для решения квадратных уравнений используется специальная формула для нахождения корней.
Запомните
Чтобы решить квадратное уравнение нужно:
- привести квадратное уравнение к общему виду «ax2+ bx + c = 0».
То есть в правой части должен остаться только «0»;
- использовать формулу для корней:
Запомните!
Выражение «b2− 4ac», которое находится под корнем, принято называть дискриминантом и обозначать буквой «D».
По-другому, через дискриминант формулу нахождения корней квадратного уравнения можно записать так:
где «D = b2− 4ac»
В зависимости от знака «D» (дискриминанта) квадратное уравнение может иметь два, один или ни одного корня. Рассмотрим все три случая.
Iслучай
D > 0
(дискриминант больше нуля)
2x2+ 5x −7 = 0
D = b2− 4ac
D = 52− 4 · 2 · (−7)
D = 25 + 56=81
D > 0
D = b2− 4ac
D = 52− 4 · 2 · (−7)
D = 25 + 56=81
D > 0
Вывод: когда «D > 0» в квадратном уравнении два корня.
II случай
D = 0
(дискриминант равен нулю)
16x2− 8x + 1 = 0
D = b2− 4ac
D = (−8)2− 4 · 16 · 1
D = 64 − 64
D = 0
D = b2− 4ac
D = (−8)2− 4 · 16 · 1
D = 64 − 64
D = 0
Вывод: когда «D = 0» в квадратном уравнении один корень.
IIIслучай
D < 0
(дискриминант меньше нуля)
9x2− 6x + 2 = 0
D = b2− 4ac
D = (−6)2− 4 · 9 · 2
D = 36 − 72
D = −36
D < 0
D = b2− 4ac
D = (−6)2− 4 · 9 · 2
D = 36 − 72
D = −36
D < 0
Вывод: когда «D < 0» в квадратном уравнении нет корней.
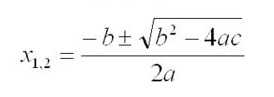
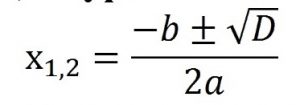
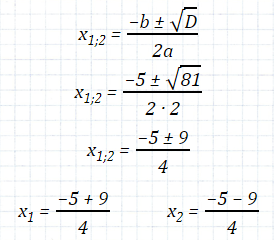
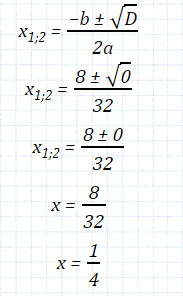
Юлия Терентьева