Решение обыкновенных дифференциальных уравнений в Wolfram|Alpha

Решение дифференциальных уравнений с выводом результатов в пошаговом представлении (функция «Show steps» — Показать шаги) является одной из важных особенностей Wolfram|Alpha. Wolfram|Alpha в большинстве случаев может помочь в решении дифференциальных уравнений различного уровня сложности, начиная от простейших дифференциальных уравнений первого порядка с разделяющимися переменными (separable equations ) и включая более сложные уравнения, для решения которых служат, например, методы операционного исчисления, использующие преобразование Лапласа.

Чтобы решить дифференциальное уравнение с помощью Wolfram|Alpha достаточно ввести его в систему.  Для ввода символа производной используется знак апострофа » ‘ «, но не кавычки (!). Для определенности можно добавить перед уравнением поисковое предписание solve (хотя, во многих случаях, это и не обязательно).

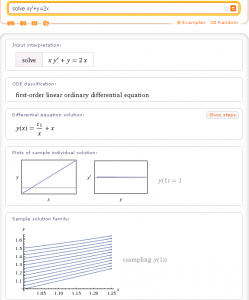
• solve xy’+y=2x

Как видим, Wolfram|Alpha сначала определяет (классифицирует) этот пример, как обыкновенное линейное дифференциальное уравнение первого порядка, затем выводит общее решение данного уравнения, график частного решения, удовлетворяющего условию y(1)=1, а также семейство интегральных кривых данного уравнения.

Чтобы получить детальное пошаговое решение, используйте кнопку «Show steps«:

Попробуйте получить аналогичным образом, решение дифференциального уравнения Бернулли:

• solve 2xy’+y=x^2y^3
• solve y’-2y/x=-x^2y^2

Wolfram|Alpha позволяет также получать решения дифференциальных уравнений второго и высших порядков. Например, так выглядит решение линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами:

• solve y’ ‘ + 2y’ +y= 54x^2e^(2x)sin(3x)

Самостоятельно найдите решение дифференциального уравнения 3-го порядка :

• solve y’ ‘ ‘ = y.