Основные понятия:
Запись и чтение десятичной дроби
Таблица разрядов
Представление обыкновенной дроби и смешанного числа в виде десятичной дроби
Представление десятичной дроби в виде обыкновенной дроби или в виде смешанного числа
На страницу урока →
Запись и чтение десятичной дроби
Часто мы встречаемся с дробями, со знаменателями 10, 100, 1000 и т.д.
Например, 1 г =1/1000 кг, 1мм =1/10 см и т.д.
Числа со знаменателями 10, 100, 1000 и т. д. договорились записывать без знаменателя.
Сначала пишут целую часть, а потом числитель дробной части. Целую часть отделяют от дробной части запятой.
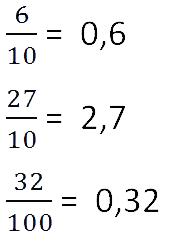
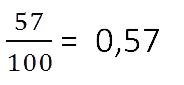
Любое число, знаменатель дробной части которого выражается единицей
с одним или несколькими нулями, можно представить в виде десятичной дроби.
Обрати внимание!!!
После запятой числитель дробной части должен иметь столько же цифр, сколько нулей в знаменателе.
Таблица разрядов
Десятичная дробь, как и любое число, состоит из цифр (0,1,2,3,4,5,6,7,8,9).
Место каждой цифры в числе важно: оно определяет разряд числа.
Десятичная дробь состоит из целой части (все цифры до запятой) и дробной части (все цифры после запятой).
Целую часть десятичной дроби можно разбить на разряды также, как и натуральные числа: единицы, десятки, сотни, тысячи и т. д.
Дробную часть десятичной дроби разбивают на разряды так:
десятые (в знаменателе обыкновенной дроби 10), сотые (в знаменателе обыкновенной дроби 100), тысячные (в знаменателе обыкновенной дроби 1000) и т.д.
Таблицу разрядов можно дополнить любым нужным количеством столбцов.
1-й разряд после запятой — разряд десятых,
2-й разряд после запятой — разряд сотых,
3-й разряд после запятой — разряд тысячных,
4-й разряд после запятой — разряд десятитысячных,
5-й разряд после запятой — разряд стотысячных,
6-й разряд после запятой — разряд миллионных,
7-й разряд после запятой — разряд десятимиллионных,
8-й разряд после запятой — разряд стомиллионных.
Пример:
Запишем в таблицу разрядов числа: 25,5701; 13,827; 3,9; 48,65.
| |
Десятки |
Единицы |
Десятые |
Сотые |
Тысячные |
Десятитысячные |
| 25,5701 |
2
|
5
|
5
|
7
|
0
|
1
|
| 13,827 |
1
|
3
|
8
|
2
|
7
|
|
| 48,65 |
4
|
8
|
6
|
5
|
|
|
| 3,9 |
|
3
|
9
|
|
|
|
Представление обыкновенной дроби и смешанного числа в виде десятичной дроби
Чтобы представить обыкновенные дроби в виде десятичных дробей, их сначала
расширяют на такое число, чтобы в знаменателе получалась разрядная единица (10, 100, 1000 и т.д.)
Обрати внимание!
Не все обыкновенные дроби можно перевести в десятичную дробь.
Например, дроби 1/3 , 2/7 , 51/9 нельзя расширить так, чтобы в знаменателе получилось
число 10, 100, 1000и т.д. Такие дроби будут рассматриваться в старших классах.
Представление десятичной дроби в виде обыкновенной дроби или в виде смешанного числа
На практике чаще используют десятичные дроби, но, когда в задаче встречаются и обыкновенные, и десятичные дроби, то следует перейти к одному виду дробей (перевести десятичные дроби в обыкновенные или обыкновенные в десятичные). Не всегда обыкновенную дробь можно перевести в десятичную, поэтому десятичную переводят в обыкновенную.
При переводе десятичной дроби в обыкновенную в числителе дроби записывают число,
стоящее после запятой, а разрядная единица в знаменателе (10, 100, 1000 и т.д.)
содержит столько же нулей, сколько знаков после запятой в десятичной дроби.
Переведём десятичные дроби 0,3; 0,17; 0,231; 0,0007 в обыкновенные.
В первой дроби 0,3 один знак после запятой, в знаменателе — 10.
В числе 0,17 два знака после запятой, в знаменателе — 100 и т.д.
0,3=3/10
0,17=17/100
0,231=231/1000
0,0007=7/10000
Если десятичная дробь содержит целую часть, то её переводят в смешанное число и целую часть записывают перед дробной.




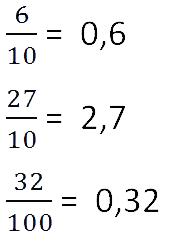







Кошевой Семён