Теорема Пифагора:
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Доказательство:
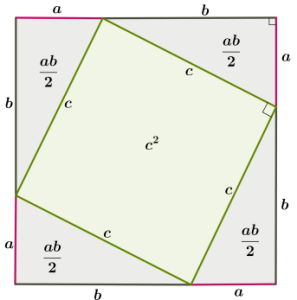
1. Построим квадрат, сторона которого равна сумме катетов данного треугольника a+b. Площадь квадрата равна (a+b)2:
2.Проведем гипотенузы c:
Стороны четырёхугольника равны c, а углы — прямые, так как острые углы прямоугольного треугольника в сумме дают 90°, то угол четырёхугольника также равен 90°, потому что вместе все три угла дают 180°.
Следовательно, площадь квадрата состоит из четырёх площадей равных прямоугольных треугольников и площади квадрата, образованного гипотенузами
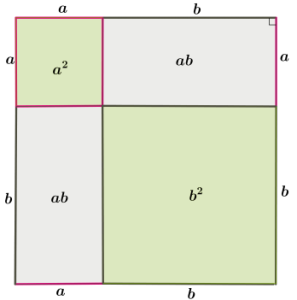
3. На двух сторонах квадрата поменяем местами отрезки a и b, при этом длина стороны квадрата не меняется.
Теперь площадь квадрата можем сложить из двух площадей квадратов, образованных катетами a и b и двух площадей прямоугольников:
4. Из этого следуют выводы:
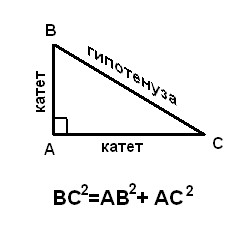
4ab:2=2ab и c²=a²+b², что и является одним из доказательств теоремы Пифагора.
Продолжите фразы:
«Сегодня на уроке я повторил…»
«Сегодня на уроке я узнал…»
«Сегодня на уроке я научился…»
Татьяна Пронина