Подготовка к изучению нового материала

Какую прямую называют секущей?

Какую прямую называют хордой?

Какая прямая является касательной к окружности?

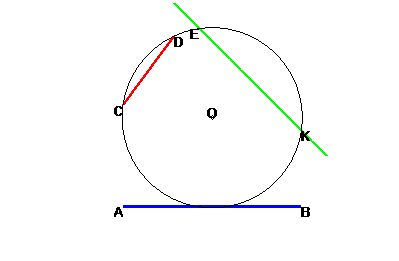
Найдите на рисунке хорду, касательную и секущую прямые.

Ответы:

Секущая — это прямая, которая пересекает в двух точках данную кривую.

Хорда— это участок секущей (отрезок), который лежит между двумя точками пересечения с кривой.

Касательная к окружности — прямая, имеющая с окружностью единственную общую точку.

Назовите признаки подобия треугольников.

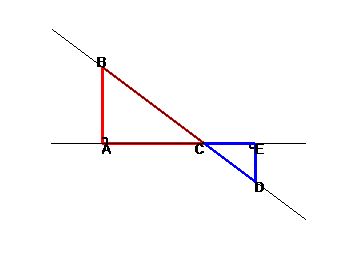
Являются ли данные треугольники подобными?

Ответы:

Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного пропорциональны сходственным сторонам другого треугольника.

 Признаки подобия треугольников: 

Первый: eсли два угла одного треугольника соответственно равны двум углам другого треугольника, то треугольники подобны.

Второй: eсли угол одного треугольника равен углу другого треугольника, а стороны, образующие этот угол, пропорциональны в равном отношении, то такие треугольники подобны. 

Третий: eсли три стороны одного треугольника соответственно пропорциональны

трем сторонам другого, то такие треугольники подобны.

 Изучение нового материала

Рассмотрим сначала секущую АС, проведенную из внешней по отношению к данной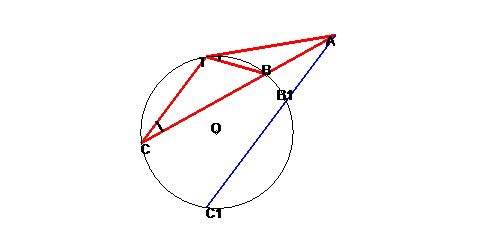

окружности точки А. Из той же точки проведем касательную АТ. Будем называть отрезок между точкой А и ближайшей к ней точкой пересечения с окружностью внешней частью секущей (отрезок АВ), отрезок же АС до более далекой из двух точек пересечения — просто секущей. Отрезок касательной от А до точки касания также коротко называем касательной. Тогда справедлива

Теорема. Произведение секущей на ее внешнюю часть равно квадрату касательной.

Доказательство. Соединим точку T c B и C. Треугольники ACT и ВТ А подобны, так как угол при вершине А у них общий, а углы ACT и BTA равны, поскольку оба они измеряются половиной одной и той же дуги ТВ. Следовательно, AC:AT=AT:AB. Отсюда получаем требуемый результат:

AC · AB=AT².

Касательная равна среднему геометрическому между секущей, проведенной из той же точки, и ее внешней частью.

Следствие. Для любой секущей, проведенной через данную точку А, произведение ее длины на внешнюю часть постоянно:

AC · AB=AC1· AB1.

 Рассмотрим теперь хорды, пересекающиеся во внутренней точке. Справедливо утверждение:          если две хорды пересекаются, то произведение отрезков одной хорды равно

 произведению отрезков другой (имеются в виду отрезки, на  которые хорда разбивается 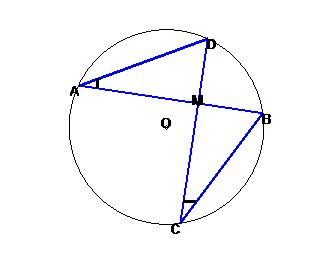точкой пересечения).

Так, хорды АВ и CD пересекаются в точке М, и мы имеем AM · MB=CM · MD.

Иначе говоря,

для данной точки М произведение отрезков, на которые она разбивает любую проходящую через нее хорду, постоянно.

Для доказательства заметим, что треугольники МВС и MAD подобны: углы 

СМВ и DMA вертикальные, углы MAD и МСВ опираются на одну и ту же дугу. Отсюда находим

MD:BM=AM:MC,

или

AM · MB=CM · MD,

что и требовалось доказать.