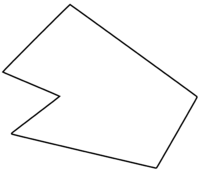
Определение многоугольника:
Многоугольником называется фигура у которой:
а)Смежные отрезки не лежат на одной прямой
б) несмежные отрезки не имеют общих точек
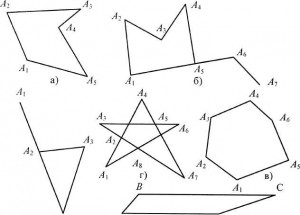
Элементы многоугольника:
Вершины многоугольника — это точки A, B, C, D… Две вершины принадлежащие одной стороне называются соседними.
Стороны многоугольника— это отрезки из которых составлен многоугольник.
Диагональ— это отрезок соединяющий две несоседние вершины.
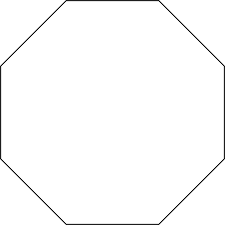
Многоугольник называют выпуклым, если он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины.
 mnogoygolnik_v
mnogoygolnik_v
Найдем сумму углов выпуклого n-угольника А1А2…Аn.
Проведем из вершины B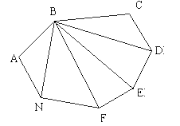 все диагонали. Получим n-2 треугольника.
все диагонали. Получим n-2 треугольника.
Сумма углов этих треугольников равна сумме углов многоугольника,
поэтому (n-2)·180°.
Сумма углов выпуклого n-угольника вычисляется по формуле (n-2)·180°.
№364,365(б,г), 367













Губашева Анастасия