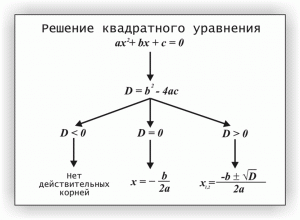
Квадратное уравнение — уравнение вида ax2 + bx + c = 0, где a, b, c — некоторые числа (a ≠ 0), x — неизвестное. называется первым коэффициентом; называется вторым коэффициентом; — свободным членом.
Пример 1) 2×2+5x-3=0.
Решение. a=2; b=5; c=-3.
D=b2— 4ac=52-4∙2∙(-3)=25+24=49=72>0; 2 действительных корня.
Пример 2) 4×2+21x+5=0.
Решение. a=4; b=21; c=5.
D=b2— 4ac=212— 4∙4∙5=441-80=361=192>0; 2 действительных корня.
3x2 + 12 x — 420 = 0
-x2 + 18 x — 80 = 0
2x2 — 4 x — 286 = 0
-3x2 — 69 x — 378 = 0
-3x2 — 21 x = 0
- 3x2 − 12x + 18 = 0;
- −4x2 + 32x + 16 = 0;
- 1,5x2 + 7,5x + 3 = 0;
- 2x2 + 7x − 11 = 0.
x2 − 9x + 20 = 0
x2 + 2x − 15 = 0
x2 + 5x + 4 = 0
x2 − 9x + 14 = 0
x2 − 12x + 27 = 0
3x2 + 33x + 30 = 0
1) ____ — это значение переменной

2)____называют квадратное уравнение, в котором старший коэффициент равен единице.
3)____ называют такое квадратное уравнение, все коэффициенты которого отличны от нуля.
4)____ называется такое квадратное уравнение, в котором хотя бы один из коэффициентов, кроме равен нулю.




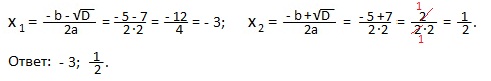
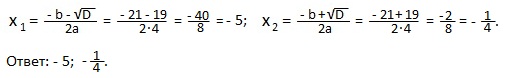










Максим Коваль