Система счисления — это знаковая система, в которой приняты определенные правила записи чисел. Знаки, с помощью которых записываются числа (рис. 1.1), называются цифрами, а их совокупность — алфавитом системы счисления.
Рис 1.1. Знаки, используемые для записи чисел в различных системах счисления
В любой системе счисления цифры служат для обозначения чисел, называемых узловыми; остальные числа (алгоритмические) получаются в результате каких-либо операций из узловых чисел.
Пример 1. В римской системе счисления узловые числа — это 1, 5, 10, 50, 100, 500 и 1000, обозначаемые соответственно I, V, X, L, C, D, M.
Виды систем счисления:
- унарная система;
- непозиционная система;
- позиционная система.
В унарной системе счисления для записи любых чисел используется всего один символ — палочка, камушек, узелок и т.д (рис 1.2.).
В непозиционной системе счисления количественное значение цифры в числе не зависит от ее положения в записи числа. В большинстве непозиционных систем счисления числа образуются путем сложения узловых чисел.
Пример 2. В древнеегипетской системе счисления числа 1, 2, 3, 4, 10, 13, 40 обозначались соответственно следующим образом:
В позиционной системе счисления количественное значение цифры зависит от ее положения (позиции) в записи числа. Основание позиционной системы счисления равно количеству цифр, составляющих ее алфавит.
Какая система здесь используется?
Основанием позиционной системы счисления может служить любое натуральное число q>1. Алфавитом произвольной позиционной системы счисления с основанием q служат числа 0, 1, …, q-1, каждое из которых может быть записано с помощью одного уникального символа; младшей цифрой всегда является 0.
В позиционной системе счисления с основанием q любое число может быть представлено в виде:
Запись числа по формуле (1) называется развернутой формой записи.
Свернутой формой записи числа называется его представление в виде:
Пример 3. Рассмотрим десятичное число 14351,1. Его свернутая форма записи настолько привычна, что мы не замечаем как в уме переходим к развернутой записи, умножая цифры числа на «веса» разрядов и складывая полученные произведения:
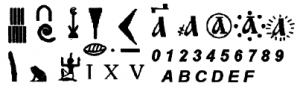
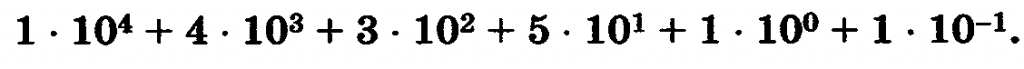
Семён Цветков