Каким бы ни было действительное число t, ему можно поставить в соответствие однозначно определенное число sin(t).
Чтобы по числу t найти значение sin(t), нужно:
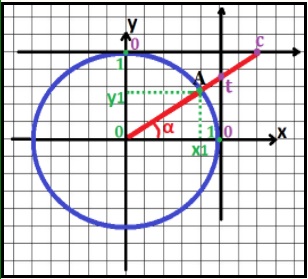
- расположить числовую окружность на координатной плоскости так, чтобы центр окружности совпал с началом координат, а начальная точка окружности попала в точку (1;0);
- на окружности найти точку, соответствующую числу t;
- найти координаты этой точки.
Эта координата и есть sin(t).
Точно также можно посчитать cos(t), tg(t) и ctg(t).
Все эти функции называют тригонометрическими функциями числового аргумента.
Есть ряд соотношений, связывающий значения различных тригонометрических функций.
Из двух последних формул легко получить соотношение, связывающее tg(t) и ctg(t):




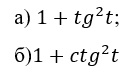
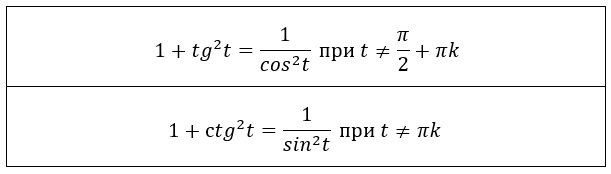
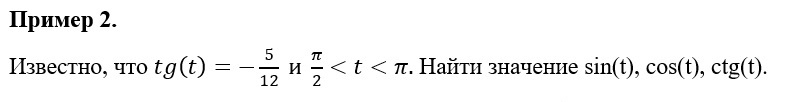







Анна Брыченкова