УРОК №8 «ОКРУЖНОСТЬ ВПИСАННАЯ В ТРЕУГОЛЬНИК»

Посмотрите на данные иллюстрации. Что общего в них можно заметить с точки зрения геометрических фигур?

 

 

Если все стороны многоугольника касаются окружности, то такая окружность называется вписанной в многоугольник. А многоугольник в этом случае называется описанным около окружности.

-вспомним   теорему о биссектрисе угла, сформулируйте её.

-теперь сформулируйте обратную теорему

-сформулируйте свойство биссектрис треугольника.
-А теперь сформулируем и докажем теорему об окружности, вписанной в треугольник

 

 

 

 

 

В любой треугольник можно вписать окружность и только одну.

 

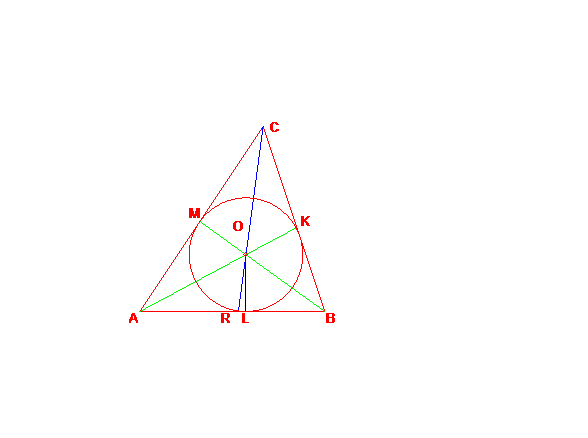
дан треугольник АВС и окружность с центром в точке О,которая является точкой пересечения биссектрис треугольника и радиусом OL (где OL перпендикулярен AB).

Докажем, что  окружность вписана в треугольник АВС.
Дано: АВС, окружность с центром в точке О.
Доказать: окружность с центром в точке О вписана в треугольник АВС
Доказательство
Рассмотрим АВС. Проведем биссектрисы треугольника, пересекающиеся в точке О.

Проведем перпендикуляр  ОL  к стороне АВ. Отметим равные отрезки ОК, ОR и ОM. Скажите, почему они равны?
Ученики: потому что ОК, ОR и ОM – радиусы одной и той же окружности.
Учитель: верно, заметим АMO= АRO.
Учитель: по гипотенузе и острому углу: AO – общая, МАО=RАО, т.к. АО-биссектриса, АМО=АRО=90.
Учитель: значит, что OR=OM, аналогично можно доказать, что ОR=OK. Итак, окружность проходит через точки K, R, M, а стороны треугольника касаются окружности в точках K, R, M. Значит, окружность с центром О радиуса ОК является вписанной в АВС. Мы доказали теорему.